Quaternion的插值分析及总结

发表于

下面的内容是阅读3D数学基础后结合自己的理解的总结

Unity中应用

我们接触到的地方就是Unity的Transform组件。Transform组件维护了四元数实现方位角位的变换。但是我们也看到Transform组件提供了eulerAgnles属性，按理说里面也实现了欧拉角的，但事实并不是这样。接下来详细分析下

首先看看类似与这种操作，我们对一个GameObject实现旋转的时候，可以直接对其transform组件的eulerAngles属性赋值需要旋转的角度即可。

1
transform.eulerAngles = Vector3.zero;

这个是transform的eulerAngles的实现，可以看到其实里面直接把欧拉角转换成了四元数来处理，所以欧拉角其实只是作为一个方法的表达形式，并没有作为Transform的成员变量之类的属性来维护 (实际上也不需要，因为有了四元数之后，欧拉角和四元数就可以实现相互的转换)

1
2
3
4
5
6
7
8
void Transform::SetLocalEulerAngles (const Vector3f& eulerAngles)
{
    ABORT_INVALID_VECTOR3 (eulerAngles, localEulerAngles, transform)
     
    SetLocalRotationSafe (EulerToQuaternion (eulerAngles * Deg2Rad (1)));
  
    ...
}

我们想对一个GameObject实现旋转还可以对其的transform组件的rotation属性以四元素的方式赋值，来实现旋转。

1
transform.rotation = Quaternion.identity;

对于rotation属性，其具体实现是这样的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Transform::SetRotation (const Quaternionf& q)
{
    ...
    
    if (father != NULL)
        SetLocalRotation (Inverse (father->GetRotation ()) * q);
    else
        SetLocalRotation (q);
}

void Transform::SetLocalRotation (const Quaternionf& q)
{
    ABORT_INVALID_QUATERNION (q, localRotation, transform);
    m_LocalRotation = q;
    
   ...
}

可以看到标红色的那行，传入的四元数被赋值参数被赋值给了m_LocalRotation成员变量。

上面介绍了在Unity里面封装的Quaternion的方位与角位的情况。那么下面Quaternion里面常用到的一个叫做Lerp的方法。相应的这个方法有一个 对应的Slerp方法。那么这两个方法到底有什么区别呢？下面来看看。

线性插值和球面线性插值的原理

Lerp是用来求两个目标之前的差值，其表达式为Lerp(a, b, t)。a和b分别为起始和终点两个点，t为差值参数变量，范围在0到1之间。Lerp表示为标准的线性差值公式的话，其公式为:

1
Lerp(a, b, t) = a + (b - a) * t

代码实现着这样的:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private Quaternion LerpX (Quaternion a, Quaternion b, float t)
{
    Quaternion result;
 
    //线性的
    float k0 = 1.0f - t;
    float k1 = t;
 
    //插值
    result.w = a.w * k0 + b.w * k1;
    result.x = a.x * k0 + b.x * k1;
    result.y = a.y * k0 + b.y * k1;
    result.z = a.z * k0 + b.z * k1;
 
    return result;
}

Slerp的计算方式(里面数学公式编辑比较麻烦，干脆直接写下来上图片了):

得出了推导公式，那么代码实现就比较简单了:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
 private Quaternion SlerpX(Quaternion a, Quaternion b, float t)
 {
        Quaternion result;
 
        //利用点乘计算两个四元素夹角的cos值
        //
        //   q1 * q2 = [w1 v1] * [w2 v2]
        //
        //           = [w1 (x1 y1 z1)] * [w2 (x2 y2 z2)]
        //
        //           = w1*w2 + x1*x2 + y1*y2 + z1*z2
 
        // 这个可以参考向量点积: 两个向量的点积等于两个向量的模乘以两个向量的夹角
        // a * b = ||a|| ||b|| cosθ
        // 如果 a和b是单位向量
        // 那么 a * b = cosθ
 
        //这里a,b是单位四元数
        //   q   = [cos(θ/2) sin(θ/2)n]
        // ||q|| = sqrt(cos(θ/2)^2 + (sin(θ/2)n)^2)
        // 如果n为单位向量，则:
        //       = sqrt(cos(θ/2)^2 + (sin(θ/2)^2)
        //       = 1
        float cosOmega = a.w * b.w + a.x * b.x + a.y * b.y + a.z * b.z;
 
        if (cosOmega < 0.0f)
        {
            result.w = -a.w;
            result.x = -a.x;
            result.y = -a.y;
            result.z = -a.z;
 
            cosOmega = -cosOmega;
        }
 
        float k0, k1;
 
        if (cosOmega > 0.9999f) //线性计算
        { //Unity中为0.95f
            k0 = 1.0f - t;
            k1 = t;
        }
        else //球面平滑的
        {
            // 用三角公式 sin^2(omega) + cos^2(omega) = 1求得
            float sinOmega = Mathf.Sqrt(1.0f - cosOmega * cosOmega);
 
            // tan(omega) = sin(omega) / cos(omega)
            // omega = atan(sin(omega) / cos(omega)
            float omega = Mathf.Atan2(sinOmega, cosOmega);
 
            // 计算 1 / sin(omega)
            float oneOverSinOmega = 1.0f / sinOmega;
 
            k0 = Mathf.Sin((1.0f - t) * omega) * oneOverSinOmega;
 
            k1 = Mathf.Sin(t * omega) * oneOverSinOmega;
        }
 
        //插值
        result.w = a.w * k0 + b.w * k1;
        result.x = a.x * k0 + b.x * k1;
        result.y = a.y * k0 + b.y * k1;
        result.z = a.z * k0 + b.z * k1;
 
        return result;
 }

两种方式比较: Lerp更少的计算量，Slerp更加平滑。实际测试下使用Slerp和Lerp的运动效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
private const int mMaxDotCount = 20;
private int mCurDotCount = 0;
private float mStep = 0.05f;
  
void Start ()
{
    StartCoroutine (Loop ());
}
  
IEnumerator Loop ()
{
    Quaternion slerpStartRoation = SlerpCapsule.rotation;
    Quaternion lerpStartRotation = LerpCapsule.rotation;
  
    while (mCurDotCount < mMaxDotCount) { //只计算mMaxDotCount次
  
        //平滑表现测试
        Quaternion newSlerpRotation = SlerpX (slerpStartRoation, Targeter.rotation, mStep);
        Quaternion newLerpRotation = LerpX (lerpStartRotation, Targeter.rotation, mStep);
  
        mStep += 0.05f;
  
        GameObject lerpDot = Instantiate (LerpDotTemplate);
  
        lerpDot.transform.SetParent (null);
        lerpDot.transform.localPosition = newLerpRotation.eulerAngles;
  
        GameObject slerpDot = Instantiate (SlerpDotTemplate);
  
        slerpDot.transform.SetParent (null);
        slerpDot.transform.localPosition = newSlerpRotation.eulerAngles;
  
        SlerpCapsule.rotation = newSlerpRotation;
        LerpCapsule.rotation = newLerpRotation;

    mCurDotCount++;
              
        yield return new WaitForSeconds (0.02f);
    }
}

通过一个个的小球，我把每次Slerp和Lerp的插值画出来，形成了一个轨迹(其中红色是Slerp的插值轨迹，白色的是Lerp的插值轨迹)

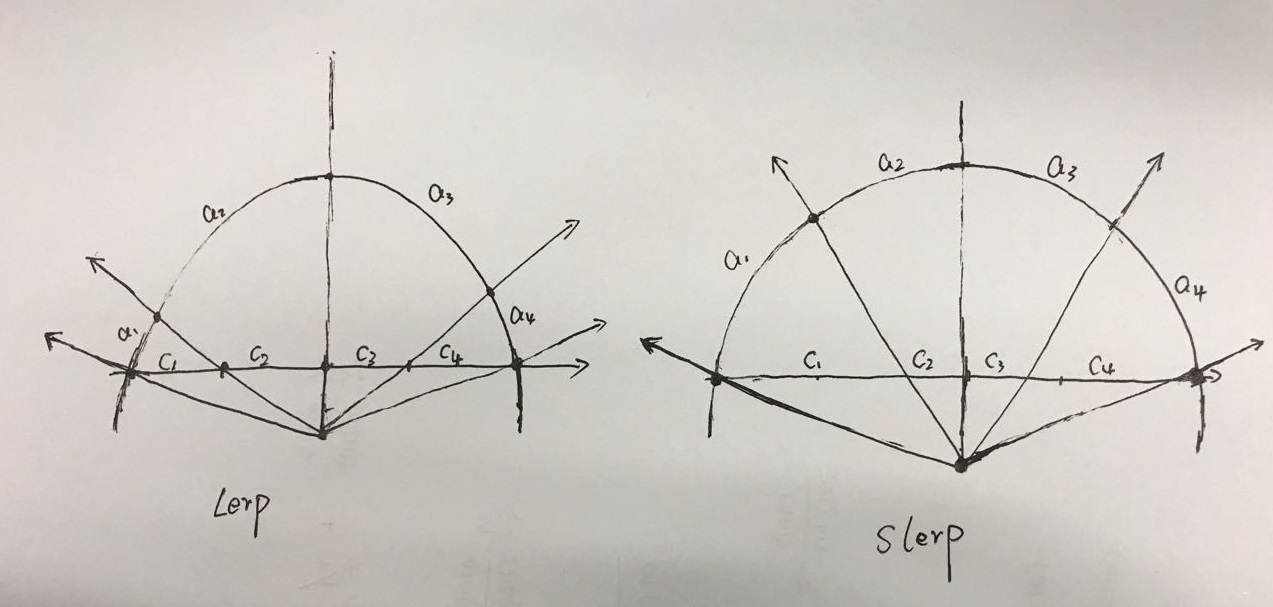
通过这个轨迹图片可以看得到(由于各个小球的Z周有一点差异，导致画面有一点透视效果)，代码Slerp的红色小球的轨迹相邻的之间距离比较均匀，但是代表Lerp的白色的小球两球之前的距离由最开始逐渐变小然后到达中间之后又开始变大。分析之后可以归结到下面两张图片中(左图描述Lerp，右图描述Slerp)。Lerp求得的是四元数在圆上的弦上的等分，而Slerp求得的是四元数载圆上的圆弧的等分(论据的图是参考的这里)。

项目中的使用问题:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private Quaternion _sphereOriginRotation;
private readonly float _rotationFactor = 0.2f;
 
void Start()
{
    _sphereOriginRotation = Sphere.rotation;
}
 
void Update()
{
    //这样用其实没有用上Slerp的球面线性差值的特性
    Sphere.rotation = Quaternion.Slerp(Sphere.rotation, Target.rotation, _rotationFactor);
 
    //上面这么写的话，其实和用Lerp得到的效果基本一样。但是Lerp的计算效率会高很多
    Sphere.rotation = Quaternion.Lerp(Sphere.rotation, Target.rotation, _rotationFactor);
         
    //要用到Slerp的球面差值的特性可以这样写,改变目标旋转的物体之前，先保存这个物体的Rotation
    Sphere.rotation = Quaternion.Slerp(_sphereOriginRotation, Target.rotation, _rotationFactor);
}