Unity 海水效果

发表于

Unity 2018.3.5.f1

越来越多的游戏中加入了类似海水的效果，效果挺不错的。这里自己也实现一个，就当做学习了。首先看实现的效果:

整个场景分为三个部分:

这里只讲解第三部分的海水是怎么实现的，其他的不在本文讲解。

针对海水我这里主要分为以下几部分来实现的。

  • 水面Mesh: 自己写了个工具，根据需要的网格数来生成Mesh面片。
  • 水波 : 用到的是常见的Gerstner波，这个在GPU Gems中有详细介绍。
  • 水面的小波纹 : 通过一个UV扰动贴图，交叉改变UV来实现。
  • 水深浅的效果 :通过计算每个水面像素的深度来改变水面透明度实现。
  • 岸边轻微的水浪效果: 这个效果是参考自lsngo ,通过一张水浪图实现的。
  • 水面的光照: 光照包含了环境光，漫反射和高光。
  • 水面的反射: 利用了一个单独的相机（剔除水所在的Layer）渲染场景到一张RT上，然后采样这张RT到水面。

水面Mesh

创建水面首先需要的是一个网格，网格的密度要适中，太小了水波波形成齿状不自然，太大了渲染的压力就会很大。我写了个简单的生成Mesh的工具，根据自己的需求来自定义网格数生成Mesh（注：网格这块我没有做LOD优化）。

水波

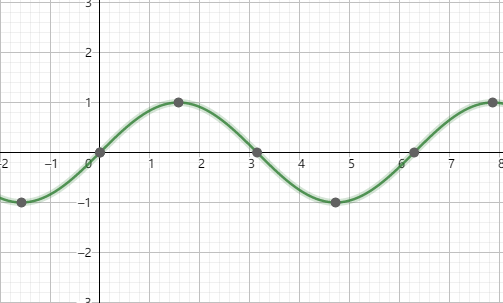
网格生成好之后着手编写shader来把这个网格渲染成水面，首先是创建摆动水波。由于正弦余弦波的特性（如下图）比较适合计算水面来回起伏的特点，很多计算水波的公式都是基于正弦余弦来演化的。

看下直接利用正弦来计算水波Mesh面波动的效果:

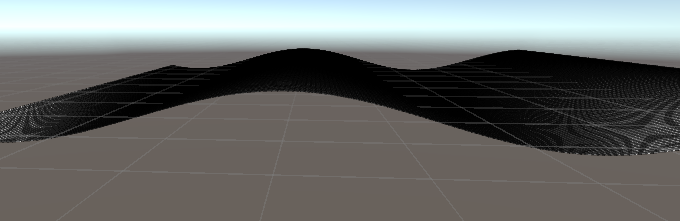
很明显，真正的海水的波不会像上图的正弦波那样的坡度那样对称缓和。gerstner更好的模拟了水波的自然形态。如下图，图中gerstner公式计算出来的波每周期左边的坡度是大于右边的坡度的，模拟水波由图片右边向左边波动的效果。

下面看看gerstner水波计算公式（详细的介绍可以参考书籍GPU Gems）: \(P(x, y, t) = \begin{pmatrix} x + \sum(Q_iA_i \times \vec{D_ix} \times cos(w_i\vec{D_i}\cdot(x,y) + \varphi_it) \\\\ y + \sum(Q_iA_i \times \vec{D_iy} \times cos(w_i\vec{D_i} \cdot(x,y) + \varphi_it)) \\\\ \sum(A_isin(w_i\vec{D_i} \cdot (x,y) + \varphi_it)) \end{pmatrix}\)

公式中x和y是水平坐标构成的面，但是在Unity中x和y是相互垂直的，所以这里的x，y对应Unity中的x，z。转换下公式:

\[P(x, z, t) = \begin{pmatrix} x + \sum(Q_iA_i \times \vec{D_ix} \times cos(w_i\vec{D_i}\cdot(x,z) + \varphi_it) \\\\ \sum(A_isin(w_i\vec{D_i} \cdot (x,z) + \varphi_it)) \\\\ z + \sum(Q_iA_i \times \vec{D_iz} \times cos(w_i\vec{D_i} \cdot(x,z) + \varphi_it)) \\\\ \end{pmatrix}\]

同理得出法线N（在这个项目里面没有用到这个法线）:

\[\vec{N} = \begin{pmatrix} -\sum(\vec{D_ix \times w_i \times A_i \times cos(w_i \times \vec{D_i} \cdot \vec{P} + \varphi_it)}) \\\\ 1 -\sum(Q_i\times w_i \times A_i \times sin(w_i \times \vec{D_i} \cdot \vec{P} + \varphi_it)) \\\\ -\sum(\vec{D_iz \times w_i \times A_i \times cos(w_i \times \vec{D_i} \cdot \vec{P} + \varphi_it)}) \\\\ \end{pmatrix}\]

上面公式中的变量说明:

  • 波长（L） ：世界空间中波峰到波峰之前的距离。波长L与角频率w的关系为： ​ \(w = 2 \pi / L\)

  • 控制波陡度的参数（Q）：对于单个的波i，Qi = 0给出正常的正弦波，表示为： ​ \(Qi = 1 / (wiAi)\) 给出尖峰的波形。应当避免选用较大的Qi值，因为它们将会在波峰上形成环。
  • 振幅（A）：从水面到波峰的高度。
  • 速度（S）：每秒钟波峰移动的距离。为了方便，把速度表示成相常数： ​ \(\varphi = S \times 2 \pi / L\)
  • 方向（D）：垂直于波阵面的水平向量。波阵面为波峰沿着它运动的面。波的状态定义为水平位置（x，z）和时间（t）的函数： ​ \(W_i（x，z，t）= A_i \times sin（\vec{D_i} \cdot（x，y）\times w_i + t \times \varphi_i）\)

编写成代码之后如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
float4 get_gerstner_wave_vertex(float4 vertex, float3 direction,float steepness, float waveLength, float speed, float amplitude)
{
	float factorW = 2 * UNITY_PI / waveLength;

	float factortrangle = factorW * direction.x + speed * _Time.y;

	float factorQ = steepness;

	float cosFactor = pow(cos(factortrangle), 2);
	float sinFactor = pow(sin(factortrangle), 2);

	float4 vertexWavePos;

	vertexWavePos.x = vertex.x + direction.x * factorQ * amplitude * cosFactor;
	vertexWavePos.y = factorQ * sinFactor;
	vertexWavePos.z = vertex.z + direction.z * factorQ  * amplitude *  cosFactor;
	vertexWavePos.w = vertex.w;

	return vertexWavePos;
}

水面的小波纹

水波的效果处理好之后，接下来实现下水面的小波纹。通俗一点说就是水面像是被风吹着有来回轻微晃动的效果。这部比较简单直接用一张凹凸贴图来实时改变水面Mesh的UV即可。但是要有来回的效果的话这里面有个方法就是对凹凸贴图进行两次采样，两次采样的UV保持不同。然后混合两个采样后的像素，把这个像素作为扰动UV的因子就可以得到想要的效果了。我用的贴图如下（也可以点这里Google一张选择自己想要的）:

计算的shader代码如下:

1
2
3
4
5
6
//法线从两个方向交叉摆动，形成一种来回的水面波纹
//不使用blue颜色，bump贴图的blue颜色太强了。
//bump的xy和zw是在顶点着色器中计算的，后面有计算代码。两者的数值是通过世界坐标和自定义的UV偏移参数确定的。
float3 bump1 = UnpackNormal(tex2D(_BumpTex, i.bump.xy)).rgr; 
float3 bump2 = UnpackNormal(tex2D(_BumpTex, i.bump.zw)).rgr;
float3 bump = (bump1 + bump2) * 0.5;

水深浅的效果

要计算水深浅的效果需要用的知识是去场景模型的深度值，取场景里的模型的深度值之前写过一篇Unity渲染的深度值获取。拿到水面底部的模型Mesh的深度值，然后用水面Mesh的深度减去底部模型Mesh深度值，得到的值就是该点水的深浅值。根据这个深浅值来改变水面颜色的透明度，即可实现水随深度变浅的效果。如下场景模型，蓝色的一层表示水面，底部是地形，从红色箭头房间其实地形的高度是越来越高的，也就是离水面的高度是越来越小的。我们需要拿到底部地形的深度值，然后用蓝色水面的深度减去它就可以得到深度。

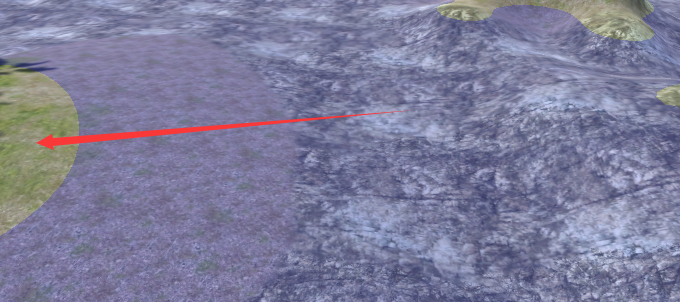
得到的深度值输出来是这个样子的，颜色越接近黑色的表示值越小也就是越浅的地方。

有了这个值可以改变像素着色器中输出的颜色的透明度来达到水越浅越透明，水越深越暗的效果了。计算的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//波的深度值
float get_wave_depth(float4 screenPos)
{
	//水面边缘的透明渐变因子  [远处 -> 岸边 颜色越来越透，形成离岸越近水越浅的效果]
	float4 screenPosNorm = screenPos / screenPos.w;

	screenPosNorm.z = (UNITY_NEAR_CLIP_VALUE >= 0) ? screenPosNorm.z : screenPosNorm.z * 0.5 + 0.5;

	//非线性的深度值 sceneDepth是GPU中的深度Buffer中的值，记录着在当前顶点渲染之前的最新的顶点深度值。
	//转换为View空间的线性值
	float linearSceneDepth = LinearEyeDepth(UNITY_SAMPLE_DEPTH(tex2Dproj(_CameraDepthTexture, UNITY_PROJ_COORD(screenPosNorm))));

 	return (linearSceneDepth - LinearEyeDepth(screenPosNorm.z));
}

水面的光照

这里给水面加了环境光，漫反射和反射。反射的光线采样自天空盒。比较简单不详细介绍了，下面是计算光照的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//计算光照
fixed3 cal_pixel_light_color(float3 bump, float3 lightDir, float3 reflect, float3 viewDir)
{
	//环境光
	fixed3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz;
	//漫反射光照
	fixed3 diffuse = _LightColor0.rgb * max(dot(bump, lightDir), 0);
	//高光
	fixed3 specular = _LightColor0.rgb * pow(max(dot(reflect, viewDir), 0), 16);

	fixed3 lightColor = ambient + diffuse + specular;

	return lightColor;
}

水面的反射

水面的反射是通过一个独立的视角翻转的相机把场景（除水面的其他部分）渲染到一个RenderTexture上，方法可以参考MirrorReflection。获得的RT效果如图:

然后把这个RenderTexture混合到水面颜色中:

1
2
3
4
5
6
7
8
9
10
//采样倒影的贴图
float4 reflectTextureUV = i.screenPos;
reflectTextureUV.xy += bump * _ReflectionDistort;
half4 reflection = tex2Dproj(_ReflectionTex, UNITY_PROJ_COORD(reflectTextureUV));

//i.reflect.w存储的是顶点相对相机的距离，这里实现距离相机越远反射率越大的效果。可以实现最远处的水面和天空盒相连的感觉。
half reflectionStrength = clamp(_ReflectionStrength*i.reflect.w*0.01, _ReflectionMinStrength, _ReflectionMaxStrength);

//混合
color.rgb = lerp(color.rgb, reflection.rgb, reflectionStrength);

添加反射之后效果就是文章开头的那副效果图的样子。对比下没加反射的效果:

以上就是整个海水效果的具体实现。下面是动画效果：

文件比较大，需要加载一会。如果有SS的话开全局模式会立即加载出来

END