PBR的学习总结

个人的理解，可能有错误的地方，欢迎指出。

测试环境：Unity2018.4.8f1（64bit）

文中画图工具：geogebra

定义

PBR（Physically Based Rendering）是一种基于物理方式旨在更加准确的模拟真实世界光照的图形渲染方法。简单点说，PBR就是计算光照射到表面时该表面射出（反射或折射）光的一套计算方法，基于物理方式在于它在计算射出光强度的时候更加注重和射入光的能量守恒。因为能量守恒，当一束光照射到某个表面时射出的光线强度会更加接近于真实世界，那么得到的光照效果就更加逼真了。这样做带来的另外一个好处在于可以提供更加直观的效果配置参数给美术人员。现在来看看PBR这套计算方法，我们称这个计算方法为反射方程（The Reflectance Equation）：

\[L_0(p, w) = L_e(p, w) + \int_{Ω} f_r(p, w_i, w_0) L_i(p, w) \cos\theta_i dw_i\]

公式里的每个符号的含义：

\(p\) ：场景中一个表面上的点
\(w_0\) ：出射光方向
\(w_i\) ：入射光方向
\(L_0(p, w)\) ：点 \(p\) 处的总共发射的辐射
\(L_e(p, w)\) ：点 \(p\) 处的预置发射的辐射
\(\Omega\) ：以点 \(p\)的法线为中心的单位半球
\(\int_{Ω} dw_i\) ：入射光在整个单位半球的积分
\(f_{r}(p, w_i, w_0)\) ：双向反射分布函数（Bidrectional Reflectance Distribution Function）
\(L_i(p, w)\)：\(p\) 点所接受的辐射
\(cos\theta_i\)：入射光照向量和 \(p\) 点的法线向量的点积（dot product），用作辐照度由于射入角度产生的衰减因子

根据这两个概念可以拆分我们的反射方程为两个部分辐射和BRDF。简单来说材质表面的PBR反射光照可以这样表示：

1	`反射光照 = 辐射率 * BRDF`

接下来详细介绍下这两部分内容，在理解这些内容之后就理解反射方程了。

辐射

真实世界中我们是怎样看到眼前的物体的呢？所有的这些物体都是因为有光照射到物体上，光在物体上经过反射（镜面反射，漫反射）进入到我们眼睛，在我们的眼睛成像于是看到了这些物体。但是光源照射到表面之后根据该表面的不同属性反射或者折射出的光的强度会不一样，比如一个表面光滑的金属铁球和一个表面带毛的网球，两个球放在同样的太阳底下你会看到金属铁球表面明显更亮，由此可以看出物体表面的光强不仅和光源有关系，还和物体本身的材质有关系。

那么我们首先来了解光的强度对材质表面的影响。需要测量对材质表面反射光的强度（或者称为辐射强度），首先我们得明白光具体含义，wikipedia上是这样介绍的：光通常指的是人类眼睛可以见的电磁波（可见光）。既然光是电磁波，那么我们就需要用电磁波的测量单位辐射能来测量光。

辐射通量（ Radiant flux ）

辐射通量定义为每单位时间发射，反射，传输或接收的辐射能总和。用公式表示为：

\[\Phi = \frac {dQ}{dt}\]

单位为焦耳/秒（J/s），或者更常用的瓦特（w）。

举个例子，光源在一个小时内发出了\(Q = 200,000J\)的辐射能，假如这个光源在每个小时内都是发出同样的能量，我们可以计算出这个光源的辐射通量：

\[\Phi = 200,000J / 3600s \approx 55.6W\]

辐照度（Irradiance ）和辐射出射度（Radiant Existance）

在辐射通量的基础上如果再给定辐射的面积\(A\)，我们可以定义这个面积内的平均辐射能量的密度，用公式表示为：

\[E = \frac{ \Phi}{A}\]

单位为：\(W/m^2\)。

如果是面积\(A\) 接受到的辐射能量密度，我们称\(E\)为辐照度。如果是面积\(A\) 发出的辐射能量密度，我们称\(E\)为辐射出射度。从公式我们可以看出，同样的辐射通量，辐射到的面积越大则辐照度越小。举个例子，如果一个点光源在所有的辐射方向上的辐射量是均匀的，如图[1]：

图[1]. 点光源均匀的辐射到四周，测量这个点光源的辐辐照度按照球的体积所接受的辐射通量来确定。

那么这个点光源的辐照度为：

\[E = \frac {\Phi}{4\pi r^2}\]

辐射强度（Radiant Intensity）

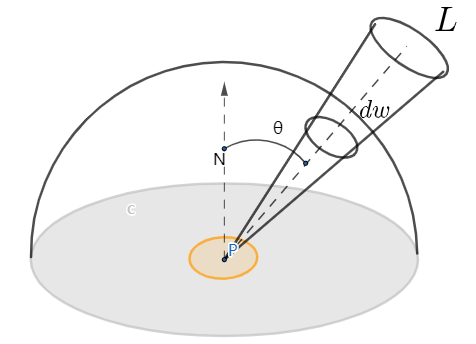
辐射强度表示一个立体角内所受到的辐射通量的总和。如图[2]，\(A\)是单位球面的一个立体角，立体角（Solid Angle）表示的是单位球面的一个截面和球心所围成的立体的体积。\(w\)表示的是辐射入射方向。从图中看辐射射入的方向和表面\(A\)是有夹角的，这会导致在表面上真正接受到的辐射面积会变小，此时辐照度可以用以下公式表示：

\[E = \frac{\Phi }{Acos\theta}\]

与辐照度和辐射出射度不同之处在于，辐射强度考虑的是受辐射的表面面积，而前者是辐射所扩散的范围，也就是体积。所以如果对于一个单位球来说的话，它的辐射强度可以表示为：

\[I = \frac{ \Phi} {4 \pi}\]

其中\(I\) 表示辐射强度，单位是\(W/sr\)。另外\(4 \pi\)表示的是球体的表面积，我们可以看做是球面上有分布均匀的无数个入射光照射到平面的点\(p\)处的辐射总和，称之为\(p\)出的辐射强度。如果是考虑有限的入射光，比如立体角所限定的范围内，那么辐射强度可以表示为以下形式：

\[I = \lim_ {\Delta w -> 0} \frac{\Delta \Phi}{\Delta w} = \frac{d \Phi}{dw}\]

将辐射通量和入射光照的函数做微分处理，得到辐射强度的通用表达式。这里解释下上面的微分操作，函数里面的辐射通量取入射光的在接近于0（但是不等于0，就是一个极值）时的增量，两者再做商，得出的就是辐射密度。

图[2] 立体角范围内接受光照

辐射率（Radiance）

辐射率表示的是光源在单位面积内，单位立体角上的辐射强度。如图[2]，单位面积\(A\)，从单位立体角\(w\)接收到的光源的辐射强度就是该面积所收到的辐射率。用公式表示为：

\[L(p, w) = \lim_{\Delta w->0} \frac{\Delta E_w(p)}{\Delta w} = \frac{dE_w(p)}{dw}\]

结合公式（8）我们可以得到在\(p\)点的辐射强度另外一种表达形式：

\[E(p, w) = \int_\Omega L_i(p, w) cos\theta dw\]

最终我们需要的辐射强度公式（10）已经得出，如果阅读到此处完全没有看明白辐射，也没有理解辐射强度公式的话，不用担心，没有任何关系。对于只想知道PBR的实际计算的话辐射知识其实可以不用了解都可以，因为后续的内容没有依赖辐射的知识，而且在反射方程实际计算的时候\(L_i(p, w)\)我们直接使用RGB值，这个RGB可以是采样一张贴图，也可以是着色器预置一个专门的变量让用户来自定义这个值。\(cos\theta\)是光照入射向量和平面的法线方向，光线由于角度入射在平面上的面积肯定变小了，而总的辐射变小了，这里的余弦值可以看做是光线由于入射角度的原因产生的衰减值。对于入射光照\(w\)的积分。在游戏中我们可以假设入射光就是一条入射光线（本文光线和光照我是混用的，因为有些句子用光照读起来更顺畅些），所以真正计算的时候可以不用做积分运算。

双向反射分布函数（BRDF）

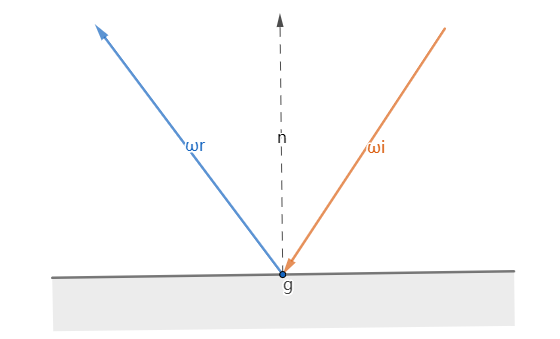
BRDF定义光在不透明表面是怎样反射的。如下图[3]，\(w_i\)是入射光方向，\(w_r\)是出射光方向（也是相机观察方向），\(n\)是法线。BRDF计算从表面沿着\(w_r\)方向发射的辐射出射度与光源沿着\(w_i\)方向入射到表面的辐照度的比值。

图[3]

用公式表示为：

\[f_r(w_i, w_r) = \frac{dL_r(w_r)}{dE_i(w_i)} = \frac{dL_r(w_r)}{L_i(w_i)cos\theta _i dw_i}\]

转换下为:

\[dL_r(w_r) = f_r(w_i, w_r)L_i(w_i)cos\theta _idw_i\]

进行下积分:

\[L_r(w_r) = \int_\Omega f_r(w_i, w_r)L_i(w_i)cos\theta_idw_i\]

得到的\(L_r(w_r)\)是\(w_r\)方向的辐射出射度，方程（7）称为反射方程（ The Reflectance Equation）或者PBR的渲染方程（The Rendering Equation）。方程关于辐射的部分在文章的上半部分已经介绍了，现在来介绍下BRDF的\(f_r(w_i, w_r)\)是怎样计算的。首先我们需要微表面（microfacets）概念，因为PBR的反射方程是基于微表面得出的。

微观表面

BRDF认为表面是没有绝对平滑的，必然有一定程度上的粗糙度，从微观层面来讲这个表面是由一个一个的微平面构成的，这些微平面的法线各异，我们称这种平面叫做微观表面（microfacets）。由于表面存在粗糙度，微观平面做不到宏观表面那样入射光照完全和法线对称的角度发生反射，微观平面上反射出去的光比较杂乱无规则。如图[4]：

图[4] 左图是微观表面，右图是宏观表面（绝对光滑）

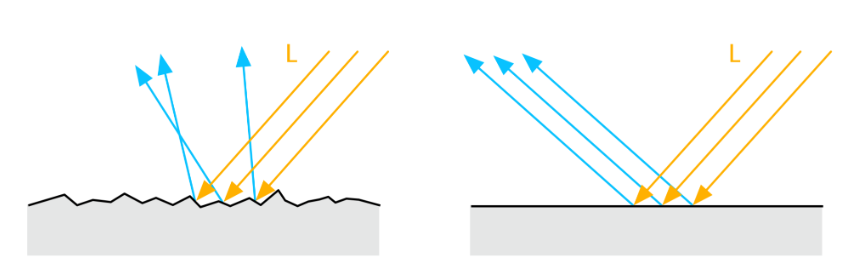
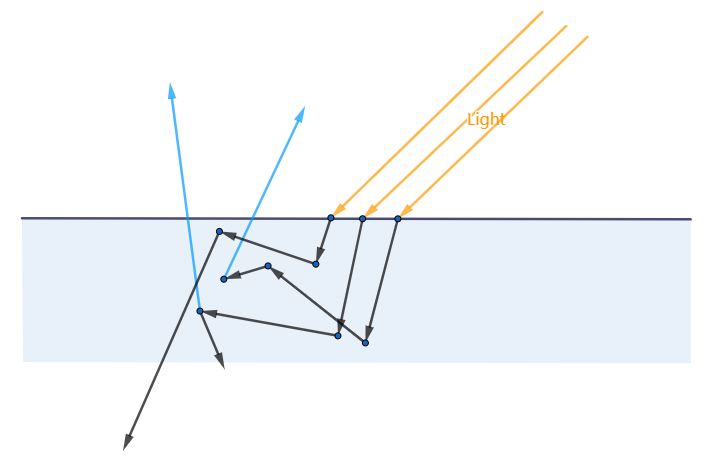
因为微观表面的凹凸不平，并不是所有反射出去的光能够进入视野，如下图[5]（暂不考虑二次反射）:

图[5]. 左图光照入射方向和视角方向比较接近，微表面的法线也是接近于视角方向的，结果是光照在微平面发射出来的光可以覆盖视角，所以从视角方向看到这部分表面是有光的。右图的情况正好相反导致从视角方向看不到表面的光照的。

BRDF对于微观表面的处理是在计算的时候加入一个粗糙度（roughness）的参数。表面的粗糙度越高，表示该表面凹凸不平的越严重，也就是微表面的法线越杂乱，那么表面反射出去的光照方向也就越不规则，实际表现出来就是整个表面看起来光照更加分散，而且光照的强度偏弱。表面的粗糙度越低，表示该表面越光滑，那么表面发射出去的关照方向更加接近一致。实际表现出来就是整个表面的光在正对着入射方向处的最明亮也比较集中，然后向四周慢慢扩散光的强度也随之慢慢降低。如下图[6]：

图[6]. 粗糙度由0.1到1.0的变化表现。

BRDF计算模型

BRDF将材质表面的光照反应分为两部分：

漫反射（diffuse）：材质表面反射或者折射出去的比较杂乱的这部分光照。
高光（specular）：材质表面以法线为中心的与入射光照对称角度反射出去的光照。

也就是说在BRDF的定义模型下，物体表面接受到光照之后会分两部分可以用表达式表示为：

\[f_r(w_i, w_r) = f_{diffuse}(w_i, w_l) + f_{specular}(w_i, w_l)\]

如下图[7]所示:

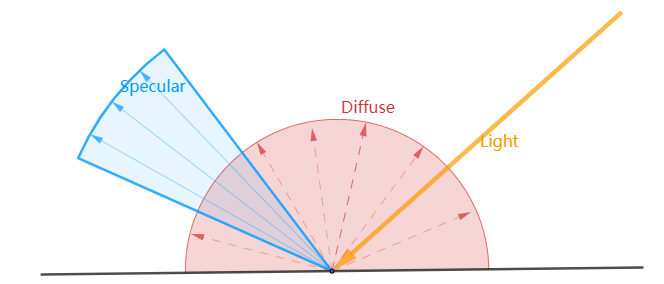
图[7]. 入射光照在经过表面反射或者折射之后归为两种模型：漫反射（Diffuse）和高光（Specular）。

考虑到光传播的能量守恒，在光照射到材质表面的时候会由于材质的粗糙度的原因一定程度上会减弱反射出去的高光的强度，如图[8]：

图[8]. 入射光照如果只考虑一次反射的话，那么像左图的情况，光照就不会反射出任何光，相当于损失了。如果考虑二次反射的话是可以反射出去并且进入到视野的,如图右。

如果粗糙度比较严重的话，光照在材质表面需要经过很多次反射才能反射出去，甚至最终反射出去的光的出射角度并不能进入到视野中去。这部分光只能算作是光衰减的部分。基于此我们对计算BRDF的公式做出下面这样的改变：

\[f_r(w_i, w_r) = k_df_{diffuse}(w_i, w_r) + k_sf_{specular}(w_r, w_r)\]

其中\(k_d\)和\(k_s\)满足：

\[k_d + k_s \leq 1\]

介绍了BRDF的计算模型之后，接下来介绍下组成BRDF模型的漫反射和高光的具体计算方式。

BRDF的漫反射（Diffuse）

漫反射其实包括两部分，一部分是由于材质表面粗糙的原因光照经过多次反射最终反射出表面，但是出射的角度比较杂乱，如图[8]所描述的。另一部分则是材质的特殊性导致折射在材质的次表面（subsurface）的光线又折射出表面形成的关照。如图[9]：

图[9]. 部分折射的光照会最终折射出表面进入视野中。

但是不是所有的材质都会有这种现象，这个就是导体与电介质两种材质的区别了。纯金属材质（导体）没有在次表面发生散射的情况。这也是现实生活中导体材质的表面看起来光照更加强分布比较集中规则，而电介质材质的表面光照相对较弱的原因。

在游戏引擎中对漫反射光照的处理一般采用的是\(lambert\)计算模型。\(lambert\)模型的用如下公式表示：

\[f_{lambert} = \frac{\sigma}{\pi}\]

\(\sigma\)为漫反射率，除以\(\pi\)的得到半球的漫反射因子。代码中计算漫反射时把漫反射颜色乘以漫反射因子，代码如下：

float brdf_lambert()
{
    return _ReflectanceRatio / UNITY_PI;
}

float3 diffuse = diffuseColor * brdf_fd_lambert();

BRDF的高光（Specular）

BRDF的高光模型这里只介绍Cook-Torrance，这是目前实用比较广泛的模型。其他的还有Phong，Blinn-Phong等模型这里就不介绍了。先来看Cook-Torrance表达式：

\[f_{specular-cooktorrance} = \frac{D(h, \alpha) G(v, l, \alpha) F(v, h, f0)}{4(n \cdot v)(n \cdot l)}\]

整个公式由三部分内容组成：

D ：正态分布函数（Normal distribution function）
G：几何阴影函数（Geometric shadowing function）
F：菲涅尔（Fresnel）

正态分布函数

由于微表面存在粗糙度的原因，每个微表面的法线方向是没有规则比较杂乱的，正态分布计算的结果模拟的是各个微表面的法线与指定方向（视角方向和光照入射方向形成的中间向量）一致的分布情况。微表面的法线和指定方向越一致，那么这个微表面的光照越强，反之则越弱。先来看一个正态分布的一个样图：

图[10]. 正态分布样图

从图中可以看到深蓝色区域所占比率为全部数值的68%，它说明了什么呢？举个很浅显的例子，读书的时候每次班级的考试成绩的分布，成绩好的和成绩差的同学总是占少数，除此之外的同学的分数你会发现都比较集中，差距比较小。这部分分数集中的同学就是图[10]中的蓝色区域。这段小范围内集中了大部分的样本，具有这种分布规律的就是正态分布。那么为什么用正态分布函数来模拟计算微表面的粗糙度呢？很简单啊，因为经过实验表面微表面的法线分布情况正好接近于正态分布。

接着看正态分布的表达式（正态分布的表达式有很多，这里使用 Trowbridge-Reitz GGX）：

\[D_{GGX}(h, \alpha) = \frac{\alpha^2}{\pi ((n \cdot h)^2)(\alpha^2-1)+1)^2}\]

表达式中的各个变量的含义：

\(\alpha\)：粗糙度。
\(h\)：视角向量（或者光照的出射向量）和光照入射向量的中间向量（ \(half = normal + lightDir\)）。
\(n\)：法线向量。

转换成代码：

float brdf_specular_ndf_ggx(float NLhalf, float roughness)
{
    //这里的a并不是公式中的alpha，只是计算时的临时变量。
    float a = NLhalf * roughtness;
    float k = roughness / (1.0 - NLhalf * NLhalf + a * a);
    return k * k * (1.0 / PI);
}

代码里面计算的时候是把表达式展开来计算的，这样计算的好处在于减少了分母中不必要的相同的计算（k值的计算），计算更高效。

几何阴影函数

几何阴影函数计算的是光照在微平面被遮蔽形成的阴影的效果，如图[5]中右图，视角方向看过去的表面形成遮蔽，光照被微表面的凹凸起势正好挡住了，正好形成阴影。

几何阴影函数表达式：

\[G(v, l, \alpha) = \frac{2(n \cdot l)}{n \cdot l + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot l)^2}} \frac{2(n \cdot v)}{n \cdot v + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot v)^2}}\]

表达式中的各个变量的含义：

\(v\)：视角向量。
\(l\)：光照向量。
\(n\)：法线向量。
\(\alpha\)：粗糙度。

之前看Unity的BRDF渲染的着色器的代码的时候一直不明白它的计算代码，它的计算代码是这样的（省略了很多细节代码）：

// Main Physically Based BRDF
// Derived from Disney work and based on Torrance-Sparrow micro-facet model
//
//   BRDF = kD / pi + kS * (D * V * F) / 4
//   I = BRDF * NdotL
//
half4 BRDF1_Unity_PBS (half3 diffColor, half3 specColor, half oneMinusReflectivity, half smoothness,
	half3 normal, half3 viewDir,
	UnityLight light, UnityIndirect gi)
{
    ...
#if UNITY_BRDF_GGX
	half V = SmithJointGGXVisibilityTerm (nl, nv, roughness);
	half D = GGXTerm (nh, roughness);
#endif
    half specularTerm = V*D * UNITY_PI; // Torrance-Sparrow model, Fresnel is applied later
    ...
    half3 color =   diffColor * (gi.diffuse + light.color * diffuseTerm)
                    + specularTerm * light.color * FresnelTerm (specColor, lh)
					+ surfaceReduction * gi.specular * FresnelLerp (specColor, grazingTerm, nv);

	return half4(color, 1);
}

通过函数说明可以看到Unity计算BRDF的公式

\[BRDF = \frac{ \frac{kD} {\pi} + kS (D V F) }4\]

不明白为啥高光部分计算\(D V F\)，\(V\)和\(G\)究竟是什么关系？特地查找了资料发现有人也在问这个问题where-come-from-about-unity-brdf-function，可惜回答里没有给出真正的具体的答案来解释清楚这个问题。其实很简单，上面给出了几何阴影函数之后我们可以带入到高光计算函数（现在还没介绍\(Fresnel\)，没有任何关系，而且\(Fresnel\)很好理解）。带入到高光计算函数中你会发现，高光计算函数的分母和几何阴影函数的分子\(4(n\cdot l)(n \cdot v)\)正好可以抵消掉，抵消掉之后我们用一个全新的符号来代替几何阴影函数，那就用\(V\)吧。全新的高光计算函数：

\[f_{specular-cooktorrance} = D(h, \alpha) V(v, l, \alpha) F(v, h, f0)\]

Unity的BRDF的公式就是这样得来的，得到的新的几何阴影函数如下：

\[V(v, l, \alpha) = \frac{1}{n \cdot l + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot l)^2}} \frac{1}{n \cdot v + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot v)^2}}\]

用代码表示如下：

float brdf_specular_gsf_smith(float dotV, float roughness2)
{
    return = 1 /(dotValue + sqrt(dotV * dotV * (1 - roughness2) + roughness2));
}

float brdf_specular_gsf_ggx(float NdotL, float NdotV, float roughness)
{
    float a2 = roughness * roughness;
	float ggx_l = brdf_specular_gsf_smith(NdotL, a2);
    float ggx_v = brdf_specular_gsf_smith(NdotV, a2);
    return ggx_l * ggx_v;
}

菲涅尔

先来看一张湖面景色图片：

图[11]

从上面的湖面景色图片中我们可以发现，距离山越近的地方水面倒影的颜色越深，距离视角位置越近倒影的颜色越浅，水下的石头也更清晰些。这种现象其实就是菲涅尔现象或者叫菲涅尔反射。菲涅尔反射描述光在两种不同折射率的介质中传播时的反射的值，通过这个值我们可以计算当光照照射到表面时，表面所反射的光的量。可以先了解下方程，这里使用 Schlick近似菲涅尔方程（一般光照计算都采用这个近似方程）： \(R(\theta) = R_0 + (R_{90} - R_0)(1-cos\theta)^5\)

\(R_0\)：光照垂直入射到材质表面时的反射比，这个值是个常数。
\(cos\theta\)：材质表面的法线向量和视角向量的余弦值。

根据公式我们可以得出反射比 \(R{\theta}\) 和视角方向有很大的关系，再来解释下图[11]中的现象。距离视角位置越远的水面位置，视角和该点位置的夹角越小，那么余弦值就越小，得出的反射比就越小。所以你看到的水面倒影越清晰，看不清水下的石头。用一张说明图来描述下，如图[12]：

图[12]

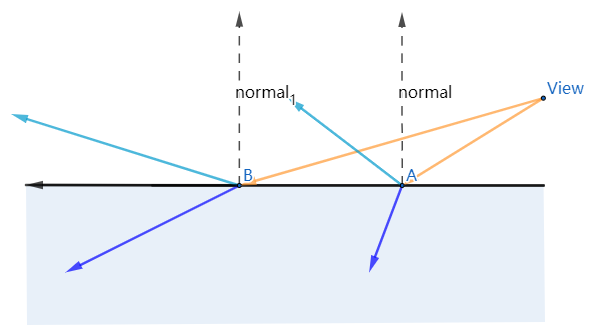
可以从近视点位置的A点和远视点位置的B来对比下反射比可以明白图[11]中的现象了。

对于菲涅尔方程中的\(R_0\)值，这个值是根据材质来定的。显示世界中一些比较常见材质的\(R_0\)值和\(cos\theta\)的菲涅尔反射比关系图如下：

图[13]

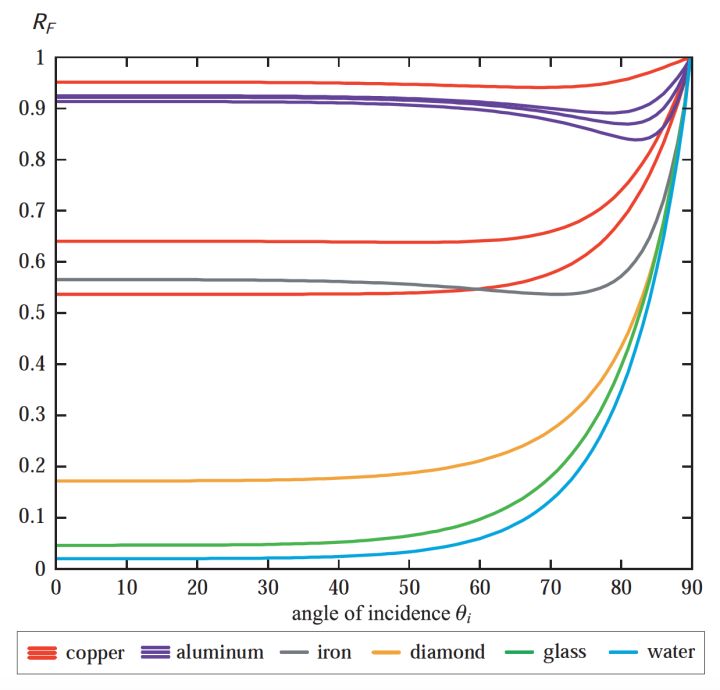
在视角向量和材质表面法线向量角度趋于\(90^\circ\)度时任何材质的反射比都趋近于1，这样在菲涅尔方程中的\(R_{90}\)我们直接可以用常数1替换。

菲涅尔反射就介绍这些，下面我们把菲涅尔反射方程转换为程序代码：

float3 brdf_fresnel_schlick(float NdotL, float3 R0)
{
    //1.0是90度时候的反射比
    return R0 + (float3(1.0, 1.0, 1.0) - R0) * pow(1 - NdotL, 5.0);
}

BRDF的内容都介绍完成了。PBR方程中现在只剩下一个内容没有提到，\(L_e(p, w)\)。放到Unity中，我们可以看看Unity的采用PBR渲染方式的Standard Shader ：

Unity里面把它当作一个材质本身一个发射的颜色，这个颜色包括自定义一个预置颜色和全局环境光照的颜色。这是一个可选项，一般简单处理的话这个值不需要也可以。

总结

到这里整个PBR的内容都介绍完成了，其实内容并不多，花费一些时间肯定能完全理解。后续我再整理出一个基于Unity实现的PBR功能的demo。

参考：