发表于

最近优化了下项目里面的UI事件系统，主要原因是随着业务量的膨胀，不管是从可维护的角度，还是从性能的角度上现有的UI设计结构已经承载不了现在的业务需求。 问题反馈或者讨论：yiliangduan@qq.com

现有的UI事件方案

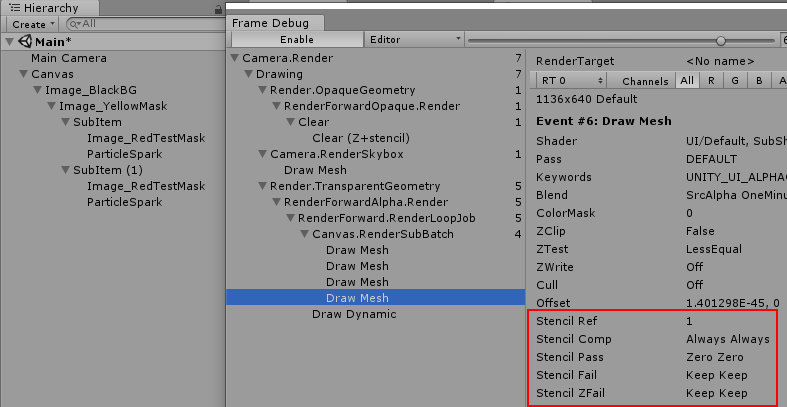
现有的UI事件分发系统以血量更新为例：

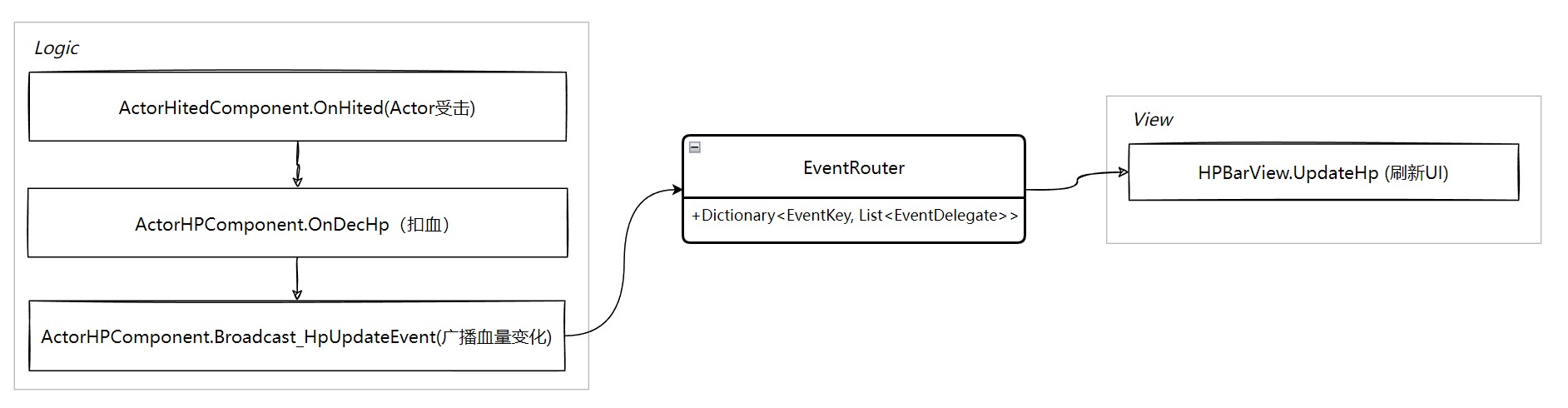
逻辑层数据变化了（血量）同步推送到表现层的UI系统来做UI刷新，伪代码如下：

1
2
3
4
5
//ActorHpComponent.cs
public void Broadcast_HpUpdateEvent(long value)
{
	EventRouter.Instance.Broadcast(EventKey.HpUpdate, actorID, value);
}

1
2
3
4
5
6
7
8
9
//HpBarView.UpdateHp.cs
public void OnHpUpdate(uint actorID, long value)
{
    //需要判断事件是否来自自己绑定的ActorID发来的
	if (actorID == selfActorID)
    {
        UpdateHp(value);
    }
}

这种模式存在的问题：

  • View可维护性差 （View指代HPBarView这种具体的UI，下同）。
  • 事件频次太高，UI刷新频次不可控。

View的可维护性差

UI的所有功能都在View中实现（HpBarView），包括事件处理、数据处理、UI更新显示。代码没有固定的结构，每个程序会在View中自由发挥，导致各种风格代码，各种造轮子。

控件刷新频次不可控

UI控件的刷新完全取决于逻辑的数据更新，如果你数据更新一帧更新多次的话，每次都会通过事件分发到UI，最后触发UI刷新。整个链路触发频率高会导致消耗上涨，虽然UGUI的Rebuild是固定每帧刷新一次的频率，但是每次SetDirty也是不小的开销（比如Text更新text时）。

1
2
3
4
5
6
7
8
9
10
11
12
//ugui Text.cs
public virtual string text
{
    set
    {
        //省略很多代码
        m_Text = value;
    	SetVerticesDirty();
        //这里会计算根据value长度来重新计算Layout,比较耗时.而且只要text更新就会计算。
    	SetLayoutDirty();
    }
}

事件频次太高

如果HpBarView的数量非常多，比如当前场景有50个HpBarView需要显示，那就是50个HpBarView在监听 EventKey.HpUpdate 事件，如果有30个Actor正好在同一帧都触发了一次Hp的更新，那就是会抛出50次 EventKey.HpUpdate 事件，那HpBarView的OnHpUpdate函数实际触发的次数：

1
30 (事件次数) * 50 (每个事件触发OnHpUpdate次数) = 150次

显然，Actor的数量越多，OnHpUpdate触发次数越高。但是我们也看到实际有效次数为 if (actorID == selfActorID) 成立的次数，也就是事件次数30次才对。

改进方案

视图View层的改进

首先需要调整的是View层的结构。我们可以参考UE5的 UMG Viewmodel系统来改造下View层结构。首先看下Viewmodel设计结构：

UMG Widget：可以看作是Unity里面的Prefab，并且是挂在了MonoBehaviour的UI脚本。

Object in Application: 可以看作是我们的逻辑层的对象。

可以看到Object 有变量更新，会先发送到ViewModels层，ViewModels层然后发到Widget，最后Widget刷新显示。相比我们自己的旧的方案，这里对UMG Widget增加了一个Viewmodel，Viewmodel的工作可以概括以下几点：

  • Viewmodel解耦了UMG Widget和 Object in Application，Object in Application层数据变化，首先是发送消息发到Viewmodel，Viewmodel负责管理这些数据，UMG Widget本身不需要有数据相关的内容，相当于把数据拆分出来单独管理。
  • Viewmodel维护了UMG Widget需要变化的组件的列表，并且把UI 组件和对应的数据变量做了绑定，数据刷新直接触发UI刷新，简化了整个UI刷新的流程。

把UE5 的Viewmodel结构应用到自己的结构中，调整了如下：

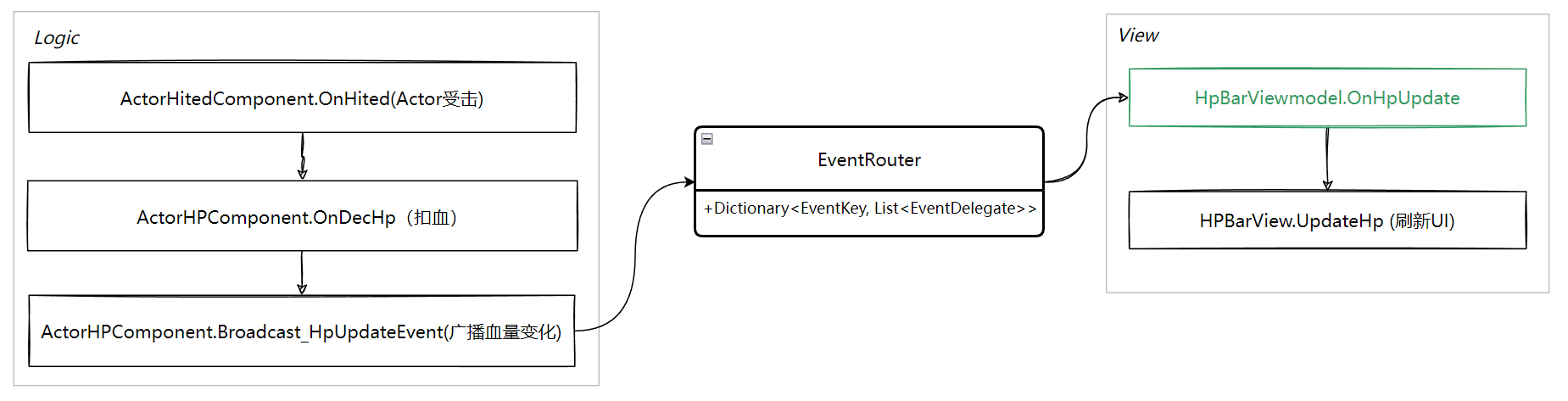
View层把空间的赋值刷新绑定到ViewModel的delegate，自己不做任何逻辑，被动响应刷新控件就行，代码规则非常明确，代码可以自动实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// HpBarView.cs 这种View代码可以全自动实现,规则非常明确  => View层
public class HpBarView : MonoBehaviour
{
    public Text hpValueText;
    //这个函数写个工具自动生成
    public void BindVariables(HpBarViewmodel viewmodel)
    {
        //绑定好ViewModel的接口。
        viewmodel.SetHpValueUI = SetHpValueUI;
    }
    public void SetHpValueUI(long hpValue)
    {
        hpValueText.text = hpValue.ToString();
    }
}

ViewModel层负责接收事件数据，并且调用绑定好的控件delegate来触发UI空间更新到最新数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//HpBarViewmodel.cs  => ViewModel层
public class HpBarViewmodel : ViewmodelBase
{
    //这种Delegate代码可以写个工具,在Prefab上通过用户选择绑定的变量和变量类型 自动生成好
    public SetHpValueUIDelegate SetHpValueUI;
    
    public void OnHpUpdate(uint actorID, long hpValue)
    {
        //Viewmodel这里维护selfActorID,HpVarView就不需要有Actor归属这类依赖数据的代码了。
        if (actorID == selfActorID)
            SetCurrentHpValue(hpValue);
    }
    public void SetCurrentHpValue(long hpValue)
    {
        SetHpValueUI(hpValue);
    }
}

至此解决了View维护性差的问题，按照规则View的代码完全是自动生成，完全是表现层代码。

更新频次改进

要控制UI刷新频次，机制上需要做的就是控制事件触发到刷新UI控件的频次。理论上来说，从源头事件发送者不发送那么多次就行，但是这对编写代码的要求和繁琐度就高了。举个例子：

受击扣血，当一个角色同一帧被10个怪攻击到主角时，会触发10次扣血操作，也就是会发送10次扣血时间到UI层，UI层如果不对事件的频次做限制的话，那么这一帧主角的血条会刷新十次，十次刷新血量从10000扣到5000，从表现上来看一帧刷新十次由10000刷到5000和一帧刷新一次由10000刷到5000肯定是一样的。不过之类也有特殊情况，就是刷新血量可能本身附带逐步刷见的动画效果，这种情况理论上来说也是触发UI一次刷新：当前值10000到目标值5000的动画是最合适的。那么怎么来处理一帧事件次数过多的问题，这里我的处理方式是两种：

  • 主动轮询获取数据方式：事件消息不直接抛给UI，而是放到一个数据池里面，UI定时轮询来获取数据。
  • 事件合并分发：事件消息不直接抛给UI，放到一个消息管理池中，每帧定时发送到对应的监听着，如果一帧收到多个事件，这合并事件的数据。

这里可能会有个疑问，为什么从逻辑层触发的UI数据，必须需要事件，是否可以直接调用UI刷新？ 对于小项目来说，这种都是无所谓的，甚至不需要考虑这方面的性能，但是对于大项目来说，逻辑和表现的分离非常有必要，而且当逻辑非常重度的时候，很多游戏逻辑直接放在单独的子线程里面跑，这种情况逻辑层的到表现层的事件可能还是作为不同线程数据交换的一种方式，关于逻辑子线程这块内容比较多，后面我单独会写几篇来介绍下。

主动轮询获取数据

这种方式的好处是每个UI可以根据自己需要的频率获取数据来刷新UI，但是缺点也很明显：

  • 很多UI更新的次数比较低频，如果一直在Tick里面轮询获取数据，本身是一种开销浪费。
  • 如果每个UI都自己写一套定时在Tick里面轮询获取数据的代码，这个代码不可控也不好维护。
事件合并分发

这种方式是基于普通的逻辑层的事件发送直接到表现层的事件响应的一个改进，这种方案也是我们项目最后使用的方案，结合上面对View层的改进，总的代码结构图如下：

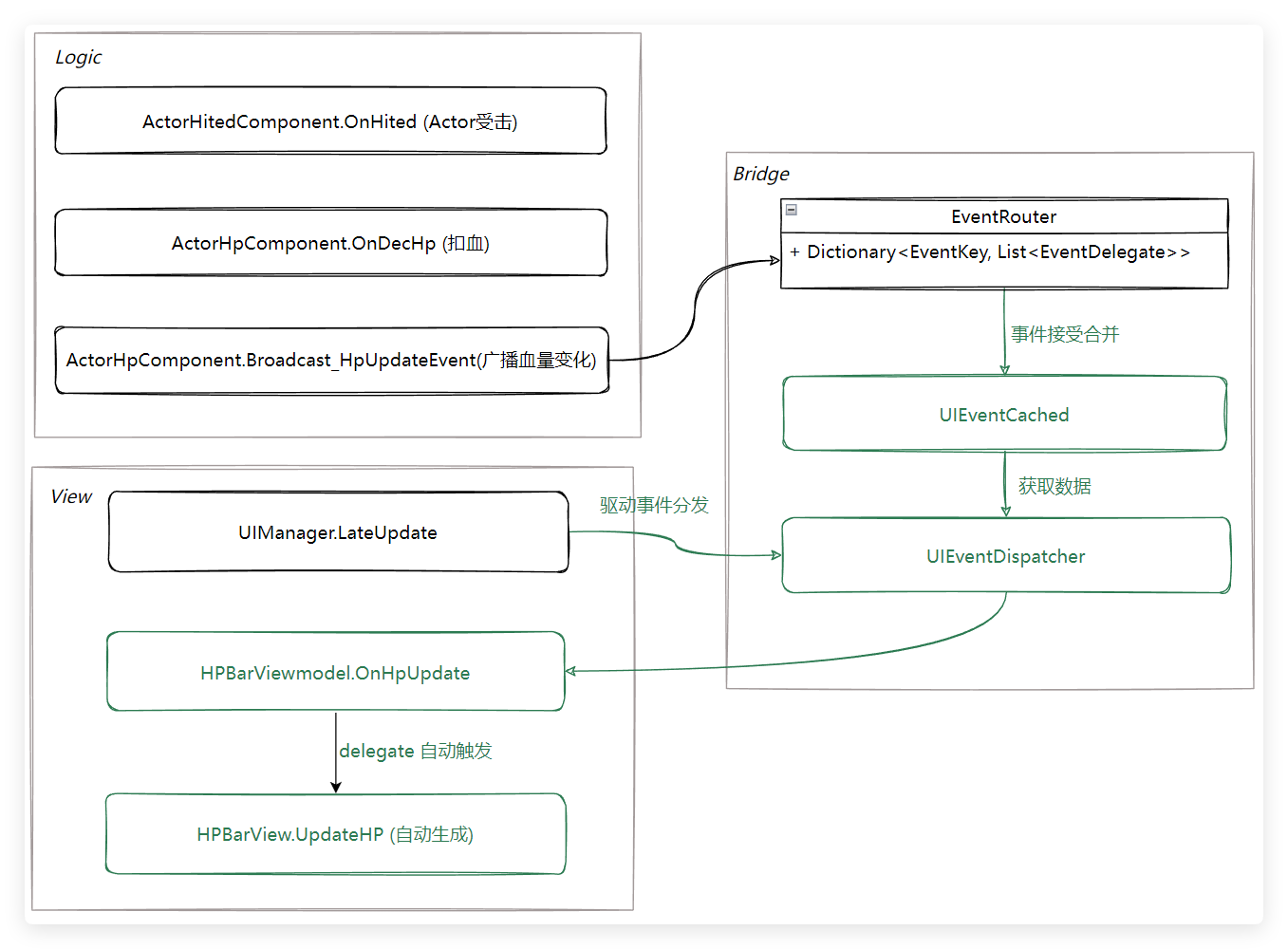
绿色标出来的是新增的逻辑，其中 Bridge 部分是事件合并分发的逻辑。改进的点主要有：

  • 业务层不需要关心事件的频次处理，只需要关注自己的界面事件监听，相比之前事件的处理方式没有额外增加复杂度。
  • 每帧的事件自动合并，到具体UI界面层的事件已经是合并之后的事件了。
  • 事件统一收束到UIManager.LateUpdate中分发，这样就非常方便在不同档位的设备上做差异化事件更新频率了。比如低端机器上可以把UI界面按照显示优先级来区分刷新优先级，低优先级刷新的事件可以两帧来分发一次等等处理。

当然事件分发器里面并不能处理所有类型的事件，也有少部分特殊情况。比扣血飘字的事件，这种事件并不能合并，因为合并之后少了扣血飘字对体验肯定是有损的。针对这种情况，事件分发器里面可以对事件最不同的归类和优先级，总得来说这种事件合并更适合血条的事件，特征点是：事件频繁，重复性高，View数量级大。

对于大型项目来说，代码规范化、可控性非常关键。这样从根本上会杜绝很多放飞自我的代码造成的性能问题，也避免项目后期很多模块需要推倒重构才能解决性能问题的困境。

引用:

  1. UMG Viewmodel
阅读全文 »

发表于

Unity2019.4.14f, UGUI

在UI（UGUI）界面的制作中，我们会遇到这种需求：在一个 ScrollRect 内显示若干个子物件UI，并且子物件UI需要显示粒子特效。这种情况我们会遇到超出 ScrollRect 需要裁剪粒子特效的问题。如：

图[1]

可以看到，超出 ScrollRect 的 SubItem 背景的 Image 裁剪掉了，但是粒子特效没有被裁减。不管是是用 RectMask2D还是 Mask 都是这样的结果。

要知道其中的原因我们先了解下 RectMask2D 和 Mask 这两个功能脚本。

RectMask2D 正如其名它只能对2D的对象进行裁剪，它是通过计算每个子节点对象的RectTransform的size来判定是否超出了设定的mask区域的，如果超出了则重新计算这个对象的大小并且调整顶点，把超出的部分丢弃掉。大概的操作如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//m_clipTargets存储的是当前RectMask2D的所有可以被裁减的子节点。
//凡是继承了IClipable的控件都是可以被裁减的，比如Image
foreach (IClippable clipTarget in m_ClipTargets)
{
    if (clipRectChanged || forceClip)
    {
        clipTarget.SetClipRect(clipRect, validRect);
    }
    var maskable = clipTarget as MaskableGraphic;
    if (maskable != null && !maskable.canvasRenderer.hasMoved && !clipRectChanged)
        continue;
 
	//只有在RectMask2D区域内的子节点才会显示。如果RectMask2D本身被裁减了，
    //那么当前RectMask2D的所有子节点也会跟着一同被裁减掉。
    clipTarget.Cull(
        maskIsCulled ? Rect.zero : clipRect,
        maskIsCulled ? false : validRect);
}

正如图[1]中的第一个item，在超出 Scrollrect 的区域背景被裁减掉了。了解了 RectMask2D的工作原理，那么很显然 RectMask2D对粒子特效裁减不了，因为 ParticleSystem 不是 UGUI 模块的代码，不可能继承了 IClippable。

Mask的实现相比于 RectMask2D 更加低层，它是利用 模板测试 (Stencil Test) 来进行裁剪的。模版测试是渲染管线（Render Pipeline）中的流程，在GPU中执行的， RectMask2D 则是在CPU中执行。模版测试的原理其实很简单：根据屏幕像素的密度给定一个对应大小的 Stencil Buffer ，每个元素只需要1byte字节，也就是最大255的精度。然后在渲染的时候 Mask（UGUI会把UI的对象转换成Mesh去渲染）对 Stencil Buffer 指定的区域（Mask设定的裁剪区域）写入指定的值（UGUI里面是写入的1），当渲染在这个区域（Stencil Buffer 的值为1）的Mask子节点的时候会进行模版测试，比较Stencil Buffer值，满足条件就继续渲染，否则丢弃掉不渲染。例如一个4x4像素的buffer，然后mask的区域是中间四个像素，假设在渲染Mask节点之前没有任何材质对Stencil Buffer进行修改，那么Stencil Buffer在渲染Mask的时候的变化是这样的：

图[2]

接着渲染Mask的子节点的时候，如果对应的像素的 Stencil值为1，则通过测试继续渲染，如果对应的像素的 Stencil值为0，则丢弃掉（相当于裁减掉了）。

既然在Mask区域只要通过测试就可以渲染，粒子特效本身也是一个Render，有单独的渲染材质，那么我们是不是可以在粒子特效的材质里添加模版测试，并且把通过测试的值设置成UGUI的Mask设置的值一致就可以了。于是在例子特效的着色器中添加模版测试的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Properties{
    //省略其他属性
	[Header(Stencil)]
	[Enum(UnityEngine.Rendering.CompareFunction)]_StencilComp("Stencil Comparison", Float) = 8
	_Stencil("Stencil ID", Float) = 0
	[Enum(UnityEngine.Rendering.StencilOp)]_StencilOp("Stencil Operation", Float) = 0
	_StencilWriteMask("Stencil Write Mask", Float) = 255
	_StencilReadMask("Stencil Read Mask", Float) = 255
}

Stencil {
	Ref[_Stencil]
	Comp[_StencilComp]
	Pass[_StencilOp]
	ReadMask[_StencilReadMask]
	WriteMask[_StencilWriteMask]
}

在Unity的Inpsector中对该着色器设置值如下：

图[3]

设置Stencil ID为1，正好是UGUI的Mask对Stencil Buffer设置的模板通过值。Stencil Comparsion值为为Equal，让当前粒子特效渲染在模版测试时 深度值等于1的时候通过，并且Stencil Operation为Keep，因为不需要改变Stencil Buffer的值。这个设置和Mask的其它UI节点一致。

修改之后发现粒子特效不可见了，也就是没有渲染出来了。间接证明了，Stencil Buffer里在粒子特效对应的像素的位置值不为1了，说明之前Mask写入的Stencil Buffer的值可能被重置掉了。这个就很奇怪了，到底哪一步做了清理工作呢？我在Unity的Frame Debugger中找到了答案。下图是 图[1]中的对象渲染时候的Frame Debug信息：

图[4]

可以看到UGUI渲染的最后一个Mesh的Stencil设置，相当于把Buffer里面为1的值重置为0了。而我们的粒子特效时在UI渲染之后渲染的（图中的Draw Dynamic），这个Mesh不渲染任何对象，纯粹做重置Stencil Buffer用的。进一步阅读了下Mask的代码，原理就清楚了。主要代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
 public virtual Material GetModifiedMaterial(Material baseMaterial)
 {
     //...省略部分代码
     //如果原先的buffer里面的值为0， 就简便处理，直接设置Buffer的值为1，然后利用另外一个Material来直接重置Buffer的值。
     if (desiredStencilBit == 1)
     {
         //设置Buffer为1的Material
         var maskMaterial = StencilMaterial.Add(baseMaterial, 1, StencilOp.Replace, CompareFunction.Always, m_ShowMaskGraphic ? ColorWriteMask.All : 0);
         StencilMaterial.Remove(m_MaskMaterial);
         m_MaskMaterial = maskMaterial;

         //重置Buffer为0的Material，这个Material就是我们在Frame Debugger中看到的UGUI渲染对象的最后一个Mesh
         var unmaskMaterial = StencilMaterial.Add(baseMaterial, 1, StencilOp.Zero, CompareFunction.Always, 0);
         StencilMaterial.Remove(m_UnmaskMaterial);
         m_UnmaskMaterial = unmaskMaterial;
         graphic.canvasRenderer.popMaterialCount = 1;
         graphic.canvasRenderer.SetPopMaterial(m_UnmaskMaterial, 0);

         return m_MaskMaterial;
     }

     //这里就考虑了在此之前Buffer的值不为0的情况，直接根据Buffer的值，然后计算出比现有Buffer值大的素数值（3，7 ...）
     //...省略

     return m_MaskMaterial;
 }

原来Mask中会创建两个Material，maskMaterial用来设置Stencil Buffer值，对应的unmaskMaterial是用来还原Stencil Buffer值的，也就是图[4]中看到的UGUI渲染的时候最后一个渲染的Mesh。到这里我们明白了为什么不管是RectMask2D和Mask都不能裁剪特效了。那么怎样可以裁剪特效呢?

第一种方法是让Mask的unmaskMaterial不重置Stencil Buffer值，而是在粒子特效渲染之后再重置Stencil Buffer的值。unmaskMaterial对Stencil的设置为StencilOp.Keep，保持不变。这种方法可以正确的裁剪掉粒子特效，测试下来也是可行的。不过需要我们修改UGUI的源码，另外一个问题是在ParticleSystem之后需要自己重置下Stencil Buffer的值。

第二种方法是使用RectMask2D来裁剪UI，我们自己来对RectMask2D区域写入指定的Stencil Buffer 值，然后对ParticleSystem的Render材质设置Stencil测试，通过测试才显示。设置如下：

图[5]

ParticleSystem的材质的设置保持和图[3]的设置一样。通过这样的设置可以看到粒子特效同样被顺利裁剪掉了。和第一种方法一样带来的问题是需要自己重置下Stencil Buffer的值。不过重置本身比较简单，可以让被裁减的 ParticleSystem 带第二个材质，第二个材质不渲染任何实际的对象，只修改Stencil Buffer值即可。

阅读全文 »

发表于

Unity2019.4.14f, UGUI

首先看UGUI自带Outline脚本实现的文本描边和利用着色器实现的文本描边效果对比（可以把图片放大点看，效果更明显一些）：

在UGUI中，对文字的描边效果的实现原理其实很简单，类似于把文字复制多份叠加在多个偏移位置上。利用UGUI的Outline实现的效果如图：

图[1]

可以看到，UGUI自带的Outline描边其实就是把原本一份Text顶点复制成四份，，四份顶点分别向四个轴偏移相同距离。具体实现是这样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public override void ModifyMesh(VertexHelper vh)
{
     //...省略部分代码
     var start = 0;
     var end = verts.Count;
     //往右上角偏移。
     ApplyShadowZeroAlloc(verts, effectColor, start, verts.Count, effectDistance.x, effectDistance.y);
     start = end;
     end = verts.Count;
     //往右下角偏移
     ApplyShadowZeroAlloc(verts, effectColor, start, verts.Count, effectDistance.x, -effectDistance.y);
     start = end;
     end = verts.Count;
     //往左上角偏移
     ApplyShadowZeroAlloc(verts, effectColor, start, verts.Count, -effectDistance.x, effectDistance.y);
     start = end;
     end = verts.Count;
     //往左下角偏移
     ApplyShadowZeroAlloc(verts, effectColor, start, verts.Count, -effectDistance.x, -effectDistance.y);

     //...省略部分代码
}

这样实现的优点是原理简单，功能实现比较方便。不过有两个明显的缺点：

  1. 描边的效果不是特别理想，可以看到图[1]中的 “这”这个字，在边缘的转角处的描边很多没有连贯起来。

  2. 因为这种描边相当于额外增加了3份的顶点数，所以描边之后带来的顶点渲染消耗也是成倍增加的。比如对于单个文字来说，描边和不描边的区别如下：

      顶点个数 三角形个数
    描边 30 10
    不描边 4 2

为了解决UGUI的Outline的第一个问题，我看到有些方法是增加重叠的三角形，让叠加的三角形能做不同的偏移来覆盖更多的边缘区域，但是这个方法会放大第二个问题的影响。因为顶点数是成倍增加的，而且一般UI界面的文字数量时比较多的，如果单个文字的顶点数成倍增加，势必会导致整个UI界面渲染的压力会极大增加。

既然增加顶点带来的收益不明显，那么我们可以考虑通过着色器来改进描边效果。因为问题的根源在于描边不连续的问题，也就是和字体边缘相同距离的像素有的有颜色，有的没有颜色。那么其实我可以不用生成多份顶点数据来做描边颜色，我可以直接在像素着色器中来根据原本的Text来计算每个文字的边缘多少个像素以内（描边宽度）的像素直接渲染为描边的颜色就可以了。

但是在像素着色器中，UGUI已经把Text处理成了一张纹理贴图，根据自己像素的坐标本身不能判断处于Text的什么位置。那么我们得换种思路，我们可以通过Text的纹理的像素来确定Text的位置，因为Text贴图有像素的地方必然是文字，没有文字的地方Alpha都是为0的。类似这样：

图[2]

红色线框内就是类似于一张Text的纹理。有文字的地方才有像素（就是文字的颜色），没有文字的地方都是透明的（Alpha为0）。这样我们在像素着色器中可以根据当前像素的透明度来判断：

  1. 如果当前渲染的像素Alpha>0，那么这个像素肯定是文字本身的像素。
  2. 如果当前渲染的像素Alpha<=0，那么这个像素肯定不是文字本身的像素。
  3. 如果当前渲染的像素的相邻像素Alpha>0，那么这个像素肯定是文字边缘像素。我们只需要把这种像素都渲染为描边颜色，那么自然得到字体的描边效果。

实现判断相邻像素需要几个条件：

  1. 到底相邻几个像素，如果只判断相邻一个像素，那么渲染得到的就是在文字的边缘有一个像素的描边。由此得知，判断几个像素决定了描边有多少个像素，也就是描边宽度。
  2. 描边的颜色。我们判断出需要描边的像素之后，我们需要有描边的颜色信息。

这两个条件是需要到像素着色器中有的值，类似于UGUI的Outline，我们可以通过MoifiedShadow组件来修改Text的顶点数据，这里我们不需要修改顶点数据，我们可以在修改顶点数据的函数里面传入我们需要的着色器参数值。

1
2
3
4
5
6
7
8
9
10
11
[RequireComponent(typeof(Text))]
public class ShaderOutline : ModifiedShadow
{
    public override void ModifyMesh(VertexHelper vh)
    {
        //...省略很多代码
        //把描边需要的  1.描边宽度 2.描边颜色  传入到着色器中
        graphic.material.SetFloat("_OutlineWidth", Mathf.Max(effectDistance.x, effectDistance.y));
        graphic.material.SetVector("_OutlineColor", effectColor);
    }
}

在着色器中，我们可以参考高斯模糊的方式处理，在着色时都采样周围多个像素的值来决定当前像素的颜色。我们就采样周围8个像素的Alpha值来确定当前像素的Alpha，如果当前像素的Alpha>0那么证明在当前像素的相邻的8个像素中肯定有其中部分像素是文字本身的像素。类似于这样（这是示意图，真正采样的时候像素密度是根据屏幕分辨率来确定的）：

当渲染像素 2 的时候，会采样到像素 1 。因为像素 1 是文字本身的像素，Alpha是大于0的。那么像素 2 最终也是Alpha大于0。计算代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//如果想要描边效果更佳平滑的话，升采样的像素点可以扩大到12或者更高，但是会带来更高的性能消耗
static const half2 UpSamplePixelCoord[8] =
{
	half2 (-1, 1),  half2 (0, 1),  half2 (1, 1),
	half2 (-1, 0),                 half2 (1, 0),
	half2 (-1, -1), half2 (0, -1), half2 (1, -1)
};

//升采样，每个像素根据周边8个像素的透明度来确定是否显示描边颜色
fixed UpSamplePixel(int index, v2f IN)
{
	half2 realOutlineWidth = _MainTex_TexelSize.xy * UpSamplePixelCoord[index] * _OutlineWidth;
	half2 pixelUV = IN.texcoord + realOutlineWidth;
	half4 pixelAlpha = (tex2D(_MainTex, pixelUV) + _TextureSampleAdd).w;
	return pixelAlpha;
}

fixed4 frag(v2f IN) : SV_Target
{
	//当前像素中心点的颜色
	fixed4 color = (tex2D(_MainTex, IN.texcoord) + _TextureSampleAdd) * IN.color;
	half4 outlineColor = half4(_OutlineColor.xyz, 0);
	int index = 0;
	for (; index < 8; ++index)
	{
		outlineColor.w += UpSamplePixel(index, IN);
	}
	outlineColor.w = clamp(outlineColor.w, 0, 1);
    //把文字本身的颜色和描边的颜色做一个过渡。
	color = lerp(outlineColor, color, color.a);
	return color;
}

我们现在可以看下利用Shader描边的效果：

可以看到描边的效果有了，但是在字体的边缘都被截掉了。这是因为文字的顶点组成的矩形区域是确定的（每个文字是由两个三角形组成的矩形，UGUI处理之后到着色器中是Mesh数据），我们增加的描边相当于加宽了文字，但是原本文字的区域我们没有加大，自然描边超出的部分就会被截掉。所以接下来我们要处理的就是把组成单个文字的两个三角形加宽，同时我们得让文字本身的大小保持不变，这样文字四周的宽度留出来给描边。类似于这样：

两个相同的文字，左边的文字的顶点矩形区域明显是比右边的是小的。右边的文字的四周空出了更多空白区域用于描边像素（空多少区域根据自己的需要描边的宽度来确定）。代码处理的方式还是通过MoifiedShadow组件来修改文字的顶点position和uv来实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public override void ModifyMesh(VertexHelper vh)
{
    //...省略很少一部分代码
    List<UIVertex> vertexStream = ListPool<UIVertex>.Get();
    vh.GetUIVertexStream(vertexStream);
    float expandWidth = Mathf.Abs(effectDistance.x * 0.5f);
    float expandHeight = Mathf.Abs(effectDistance.y * 0.5f);
    //   v1----v2
    //   | \    |
    //   |   \  |  
    //   |     \|
    //   v4----v3
    //  顺序按照vertex来确定的，一个文字由两个triangle组成，并且任意文字的vertex顺序都是相同的
    //  但是不同文字的uv的顺序不一样
    int length = vertexStream.Count;
    for (int i = 0; i < length; i += 6)
    {
        Vector2 expandPositionSize = GetExpandPositionSize(expandWidth, expandHeight);
        Vector2 shrinkUvSize = GetShrinkUvSize(vertexStream, expandWidth, expandHeight, i);
        RePackTextVertex(vertexStream, i, expandPositionSize, shrinkUvSize);
    }
    vh.Clear();
    vh.AddUIVertexTriangleStream(vertexStream);
    ListPool<UIVertex>.Release(vertexStream);
        //...省略很少一部分代码
}

代码中的 GetExpandPositionSize 比较好处理，因为文字的顶点顺序是确定的，按照固定的顺序去增加或者减去expand值，保证每个顶点的坐标向外扩即可。GetShrinkUvSize这个处理起来要稍微注意下，因为文字的UV的坐标不确定，我没有法线任何规律，也就是说两个文字的同一个顶点处，uv坐标顺序可能会不一样。这就需要自己根据每个uv的值来判断了，保证每个顶点的uv是向内缩即可，实现的原理如图（图中假设内缩大小为(0.2, 0.2)）：

我这里的代码是这样处理的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
private Vector2 ShrinkUvSize(Vector2 uv, Vector2 leftVertexUv, Vector2 rightVertexUv, Vector2 shrinkSize)
{
    float x = ShrinkValue(uv.x, leftVertexUv.x, rightVertexUv.x, shrinkSize.x);
    float y = ShrinkValue(uv.y, leftVertexUv.y, rightVertexUv.y, shrinkSize.y);
    return new Vector2(x, y);
}
/// <summary>
///   left  三个uv点关系。value：当前uv点，left：value的左边uv点，right：value的右边UV点
///   |
///   |
///  value --- right
/// </summary>
private float ShrinkValue(float value, float left, float right, float shrinkValue)
{
    if (value < left)
    {
        value -= shrinkValue;
    }
    else if (value == left)
    {
        value = value < right ? value-shrinkValue : value +shrinkValue;
    }
    else
    {
        value += shrinkValue;
    }
    return value;
}

处理了文字描边被裁减的问题之后我们再看下效果：

每个文字的边缘出现了不需要的颜色像素，因为我们修改了uv，把文字的顶点的uv值放大了，所以放大的那部分uv对应的像素原本是其他文字的像素现在被采样近来了。所以我们需要剔除掉这部分本不是当前文字的像素。这个可以直接在着色器中处理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//判断像素是否在三角形中：像素点依次和三角形的两个顶点的叉积的方向同向。
fixed IsPixelInTriangle(float3 pixelPos, float3 a, float3 b, float3 c)
{
	float z1 = cross(pixelPos - a, a - b).z;
	float z2 = cross(pixelPos - b, b - c).z;
	float z3 = cross(pixelPos - c, c - a).z;
	return z1 * z2 > 0 && z2 * z3 > 0;
}

//判断像素是否在一个Rect中，由于Rect是由两个Triangle组成，所以只需要判断顶点是否在任意一个Triangle中即可。
fixed IsPixelInRect(float3 pixelPos, float3 a, float3 b, float3 c, float3 d)
{
	return IsPixelInTriangle(pixelPos, a, b, c) || IsPixelInTriangle(pixelPos, c, d, a);
}

最后我们再看下渲染的结果：

现在已经没有问题了，而且效果还是不错的，描边比较柔和并不会出现UGUI的outline那种不连续的情况。我们对比下两种描边的效果：

再来看下两种描边的三角形数量：

总体来说利用着色器来进行描边的最终效果对于UGUI的outline的改进还是比较明显的。利用着色器来描边的方式把CPU的性能消耗转移到了GPU，因为我们需要对每个像素做8次的采样，自然就增加了GPU的性能消耗。两种方式哪种合适还得结合自己的项目需求来定。

参考：https://gameinstitute.qq.com/community/detail/114969

阅读全文 »

发表于 | 分类于

法线贴图是一种凹凸贴图（Bump Map），它可以让你将其纹理数据添加到模型，从而为模型增加表面细节（凹凸，凹槽和划痕）和光照效果。法线贴图分为两种：切线空间的法线贴图（Tangent-space normal map）和模型空间的法线贴图（Object-space normal map），两者的唯一区别正如命名那样法线所在的坐标系不同。通常情况下（游戏开发）我们使用的都是切线空间的法线贴图，所以这里介绍切线空间的法线贴图。

切线空间（Tangent space）

首先我们了解下什么是切线空间。切线空间 由Normal向量，Tangent向量和Binormal向量，三个互相垂直的向量组成。如图：

图片来源:http://intcomputergraphics.blogspot.com/2013/04/tangent-space-normal-mapping.html

Tangent和Binormal只需要满足两者互相垂直并且与顶点所在的曲面相切即可，所以任意一个三维的顶点它的Tangent和Binormal的数量时无限多个的。为了方便我们对采样法线贴图，规定切线空间的Tangent向量保持和UV坐标系的U方向一致，Binormal向量保持和UV坐标系的V方向一致，Normal方向保持和Z方向（Up方向，在Unity中这点和模型坐标或者其他坐标系不同）一致。这样对于某个顶点来说，以它为原点的切线空间就是固定的了。

法向量的存储

法向量为什么要存储在切线空间中呢？我们在Unity中使用法线贴图的时候应该有过这样的经历，同一张法线贴图会使用在不同的Mesh上。不同的Mesh的顶点和面基本上是不同的，但是却可以使用同一张贴图，这就是切线空间好处，切线空间是建立在以顶点为原点的坐标系，它不需要关心你Mesh的结构。如果你的法向量存储在模型的坐标空间，那么采样出来的法向量对于其他模型来说没办法转换到自身的模型坐标了那就没办法使用。如果是存储的是切线空间，那么可以通过对应顶点的切线空间坐标系转换到自身的模型坐标来计算光照了，或者直接在切线空间计算光照即可。

对于切线空间还有个需要注意的地方，由于平台的差异（OpenGL平台UV的V轴坐标从下往上的值为[0, 1]，DirectX平台的UV的V轴坐标从上往下的值为[0, 1]）Binormal向量可能有两个方向。为了区分不同平台的这个差异，Unity在模型导入的时候计算出一个符号标记，存储在Tangent.w变量，在自己的着色器需要计算Binormal时需要用到（Mesh存储的是每个顶点的Binormal，如果需要精确每个Fragment的Binormal，则可以通过法向量和切线向量计算得来）。计算Tangent.w的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//正交化切线向量
void OrthogonalizeTangent (TangentInfo& tangentInfo, Vector3f normalf, Vector4f& outputTangent)
{
    //tangentInfo里面带了tangent向量和binormal向量数据。
    TangentInfo::Vector3d tangent  = tangentInfo.tangent;
    TangentInfo::Vector3d binormal = tangentInfo.binormal;
    
    //1.此处省略了正交化tangent和binomal。因为导入的Mesh的tangent和binormal，normal和binormal可能不垂直。
    
    //2.此处省略tangent和binormal向量的长度异常检查。如果长度小于浮点型最小精度，则直接用标准化单位向量（如Up（0， 0，1））。

    //normalf, tangentf，binormalf是上面两步计算而来的长度大于0互相垂直向量
    //并且，这三个向量组成了切线坐标系。
    
    //先通过 normalf和tangentf计算出该平台的binormal向量
    Vector3f binormalPlatform = Cross(normalf, tangentf);
    
    //然后通过比较binormalPlatform和binormalf是否是相同方向
    float dp = Dot (binormalPlatform, binormalf);
    
    //如果两者的方向相同，则表示Mesh的binormal和当前平台采用的UV方向一致
    //就不需要flip，给tangent.w赋值为1。
    if ( dp > 0.0F)
        outputTangent.w = 1.0F;
    //反之，表示当前平台的V方向和Mesh数据里面的V方向是不同平台的标准
    //需要flip下，给tangent.w赋值为-1。
	else
		outputTangent.w = -1.0F;
}

在着色器中计算每个Fragment的Binormal的方法为：

1
2
3
//如果Mesh的Scale值为（-1， 1， 1）值，那么需要对这个Mesh以zy组成的平面做镜像，那么计算出来的binormal也是需要做镜像的，unity_WorldTransformParams.w存储的就是是否需要做镜像的符号标记
//tagent.w 是由于不同平台UV坐标轴的差异建立的符号标记
float3 binormal = cross(normal, tangent.xyz) * (tangent.w * unity_WorldTransformParams.w);

在法线贴图中，法向量的XYZ值存储在贴图的颜色通道中。Unity会分别处理贴图是否使用了压缩格式（PC平台）的情况：

  • 不压缩的情况下法线贴图对法向量的XYZ值分别存储在RGB中，值的格式为（X，Y，Z，1）。
  • 压缩的情况下又会分别根据压缩格式做不同的处理，Unity中有两种针对贴图的压缩格式：
    • DXT5，法向量的XY值分别存储在贴图的WG通道中，值的形式为（1，Y，1，X）
    • BC格式（BC5和BC7），这种格式法向量的XY值分别存储在贴图的RG通道，值的形式为（X， Y， 1， 1）。

使用这两种压缩格式法线贴图都不会存储Z值，因为法线贴图存储的法向量是单位向量，单位向量的长度为1，所以Z值可以通过XY分量计算出来（减小了贴图的存储大小，但是牺牲了GPU的性能）。计算公式如下：

\[Z = \sqrt{1 - X^2 - Y^2} \tag{1}\]

此外由于贴图通道的值的范围为[0, 1]，而标准化的法向量的值为[-1, 1]（有正负方向），所以为了把向量值作为颜色值存储在贴图中，需要把向量的值的经过变换：

\[f(N) = \frac{N+1}{2} \tag{2}\]

法向量的读取

现在来看下Unity内置着色器中解码法向量值的代码，结合之前讲的存储的方式来看解码的代码还是比较清晰的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
half3 UnpackScaleNormalRGorAG(half4 packednormal, half bumpScale)
{
    #if defined(UNITY_NO_DXT5nm)
  		 //未压缩
  		 //按照存储时的公式（2），把值还原成[-1, 1]的范围。
        half3 normal = packednormal.xyz * 2 - 1;
        #if (SHADER_TARGET >= 30)
            normal.xy *= bumpScale;
        #endif
        return normal;
    #else
  			//DXT5，BCX执行这里
        // 把w值转换到x值上，即（1，Y，1，X）变成（X，Y，1，X）
        packednormal.x *= packednormal.w;

        half3 normal;
        normal.xy = (packednormal.xy * 2 - 1);
        #if (SHADER_TARGET >= 30)
            normal.xy *= bumpScale;
        #endif
        normal.z = sqrt(1.0 - saturate(dot(normal.xy, normal.xy)));
        return normal;
    #endif
}

//bumpScale是缩放值
half3 UnpackScaleNormal(half4 packednormal, half bumpScale)
{
    return UnpackScaleNormalRGorAG(packednormal, bumpScale);
}

法线贴图为什么主要是蓝色

还有最后一个问题，为什么Unity编辑器中法线贴图看起来一般呈现的主要是是蓝色的（Unity使用的是切线空间的法线贴图，实际上模型空间的法线贴图表现没有特别的呈现主要为蓝色的现象），如图：

一个不对顶点像素产生任何作用（没有实际影响该顶点的光照计算，没有对该像素产生任何额外的表面效果）的切线空间的法向量是这样的（0， 0， 1），也就是正Up方向的单位向量。法向量的XYZ值存储到法线贴图的RGB话需要经过公式(2)转换下值的范围，转换之后为（0.5， 0.5， 1）,这个颜色值显示出来是蓝色。也就是说如果一张法线贴图每个像素都是存储的这个颜色值，那么这张法线贴图呈现出纯蓝色的。一个模型按照实际表现出来的真实细节来看，大部分情况下法向量都是接近于Up值的，少部分细节（比如脸上的皱纹边缘，地板的缝隙处）法向量的值有相对比较大点的差异，如上法线贴图就是用在墙面模型的，可以看出来砖块的交界处的颜色明显不一样。

阅读全文 »

发表于 | 分类于

个人的理解，可能有错误的地方，欢迎指出。

测试环境：Unity2018.4.8f1（64bit）

文中画图工具：geogebra

定义

PBR（Physically Based Rendering）是一种基于物理方式旨在更加准确的模拟真实世界光照的图形渲染方法。简单点说，PBR就是计算光照射到表面时该表面射出（反射或折射）光的一套计算方法，基于物理方式在于它在计算射出光强度的时候更加注重和射入光的能量守恒。因为能量守恒，当一束光照射到某个表面时射出的光线强度会更加接近于真实世界，那么得到的光照效果就更加逼真了。这样做带来的另外一个好处在于可以提供更加直观的效果配置参数给美术人员。现在来看看PBR这套计算方法，我们称这个计算方法为反射方程（The Reflectance Equation）：

\[L_0(p, w) = L_e(p, w) + \int_{Ω} f_r(p, w_i, w_0) L_i(p, w) \cos\theta_i dw_i\]

公式里的每个符号的含义：

  • \(p\) ：场景中一个表面上的点
  • \(w_0\) ：出射光方向
  • \(w_i\) ：入射光方向
  • \(L_0(p, w)\) ：点 \(p\) 处的总共发射的辐射
  • \(L_e(p, w)\) ：点 \(p\) 处的预置发射的辐射
  • \(\Omega\) ：以点 \(p\)的法线为中心的单位半球
  • \(\int_{Ω} dw_i\) ：入射光在整个单位半球的积分
  • \(f_{r}(p, w_i, w_0)\) ：双向反射分布函数（Bidrectional Reflectance Distribution Function）
  • \(L_i(p, w)\)：\(p\) 点所接受的辐射
  • \(cos\theta_i\)：入射光照 向量和 \(p\) 点的法线向量的点积（dot product），用作辐照度由于射入角度产生的衰减因子

根据这两个概念可以拆分我们的反射方程为两个部分辐射和BRDF。简单来说材质表面的PBR反射光照可以这样表示：

1
反射光照 = 辐射率 * BRDF

接下来详细介绍下这两部分内容，在理解这些内容之后就理解反射方程了。

辐射

真实世界中我们是怎样看到眼前的物体的呢？所有的这些物体都是因为有光照射到物体上，光在物体上经过反射（镜面反射，漫反射）进入到我们眼睛，在我们的眼睛成像于是看到了这些物体。但是光源照射到表面之后根据该表面的不同属性反射或者折射出的光的强度会不一样，比如一个表面光滑的金属铁球和一个表面带毛的网球，两个球放在同样的太阳底下你会看到金属铁球表面明显更亮，由此可以看出物体表面的光强不仅和光源有关系，还和物体本身的材质有关系。

那么我们首先来了解光的强度对材质表面的影响。需要测量对材质表面反射光的强度（或者称为辐射强度），首先我们得明白光具体含义，wikipedia上是这样介绍的：光通常指的是人类眼睛可以见的电磁波（可见光）。既然光是电磁波，那么我们就需要用电磁波的测量单位辐射能来测量光。

辐射通量（ Radiant flux ）

辐射通量定义为每单位时间发射，反射，传输或接收的辐射能总和。用公式表示为：

\[\Phi = \frac {dQ}{dt}\]

单位为 焦耳/秒（J/s），或者更常用的瓦特（w）。

举个例子，光源在一个小时内发出了\(Q = 200,000J\)的辐射能，假如这个光源在每个小时内都是发出同样的能量，我们可以计算出这个光源的辐射通量：

\[\Phi = 200,000J / 3600s \approx 55.6W\]

辐照度（Irradiance ）和辐射出射度（Radiant Existance）

在辐射通量的基础上如果再给定辐射的面积\(A\)，我们可以定义这个面积内的平均辐射能量的密度，用公式表示为：

\[E = \frac{ \Phi}{A}\]

单位为：\(W/m^2\)。

如果是面积\(A\) 接受 到的辐射能量密度，我们称\(E\)为辐照度。如果是面积\(A\) 发出 的辐射能量密度，我们称\(E\)为辐射出射度。从公式我们可以看出，同样的辐射通量，辐射到的面积越大则辐照度越小。举个例子，如果一个点光源在所有的辐射方向上的辐射量是均匀的，如图[1]：

图[1]. 点光源均匀的辐射到四周，测量这个点光源的辐辐照度按照球的体积所接受的辐射通量来确定。

那么这个点光源的辐照度为：

\[E = \frac {\Phi}{4\pi r^2}\]

辐射强度（Radiant Intensity）

辐射强度表示一个立体角内所受到的辐射通量的总和。如图[2]，\(A\)是单位球面的一个立体角， 立体角（Solid Angle）表示的是单位球面的一个截面和球心所围成的立体的体积。\(w\)表示的是辐射入射方向。从图中看辐射射入的方向和表面\(A\)是有夹角的，这会导致在表面上真正接受到的辐射面积会变小，此时辐照度可以用以下公式表示：

\[E = \frac{\Phi }{Acos\theta}\]

与辐照度和辐射出射度不同之处在于，辐射强度考虑的是受辐射的表面面积，而前者是辐射所扩散的范围，也就是体积。所以如果对于一个单位球来说的话，它的辐射强度可以表示为：

\[I = \frac{ \Phi} {4 \pi}\]

其中\(I\) 表示辐射强度，单位是\(W/sr\)。另外\(4 \pi\)表示的是球体的表面积，我们可以看做是球面上有分布均匀的无数个入射光照射到平面的点\(p\)处的辐射总和，称之为\(p\)出的辐射强度。如果是考虑有限的入射光，比如立体角所限定的范围内，那么辐射强度可以表示为以下形式：

\[I = \lim_ {\Delta w -> 0} \frac{\Delta \Phi}{\Delta w} = \frac{d \Phi}{dw}\]

将辐射通量和入射光照的函数做微分处理，得到辐射强度的通用表达式。这里解释下上面的微分操作，函数里面的辐射通量取入射光的在接近于0（但是不等于0，就是一个极值）时的增量，两者再做商，得出的就是辐射密度。

图[2] 立体角范围内接受光照

辐射率（Radiance）

辐射率表示的是光源在单位面积内，单位立体角上的辐射强度。如图[2]，单位面积\(A\)，从单位立体角\(w\)接收到的光源的辐射强度就是该面积所收到的辐射率。用公式表示为：

\[L(p, w) = \lim_{\Delta w->0} \frac{\Delta E_w(p)}{\Delta w} = \frac{dE_w(p)}{dw}\]

结合公式（8）我们可以得到在\(p\)点的辐射强度另外一种表达形式：

\[E(p, w) = \int_\Omega L_i(p, w) cos\theta dw\]

最终我们需要的辐射强度公式（10）已经得出，如果阅读到此处完全没有看明白辐射，也没有理解辐射强度公式的话，不用担心，没有任何关系。对于只想知道PBR的实际计算的话辐射知识其实可以不用了解都可以，因为后续的内容没有依赖辐射的知识，而且在反射方程实际计算的时候\(L_i(p, w)\)我们直接使用RGB值，这个RGB可以是采样一张贴图，也可以是着色器预置一个专门的变量让用户来自定义这个值。\(cos\theta\)是光照入射向量和平面的法线方向，光线由于角度入射在平面上的面积肯定变小了，而总的辐射变小了，这里的余弦值可以看做是光线由于入射角度的原因产生的衰减值。对于入射光照\(w\)的积分。在游戏中我们可以假设入射光就是一条入射光线（本文光线和光照我是混用的，因为有些句子用 光照 读起来更顺畅些），所以真正计算的时候可以不用做积分运算。

双向反射分布函数（BRDF）

BRDF定义光在不透明表面是怎样反射的。如下图[3]，\(w_i\)是入射光方向，\(w_r\)是出射光方向（也是相机观察方向），\(n\)是法线。BRDF计算从表面沿着\(w_r\)方向发射的辐射出射度与光源沿着\(w_i\)方向入射到表面的辐照度的比值。

图[3]

用公式表示为：

\[f_r(w_i, w_r) = \frac{dL_r(w_r)}{dE_i(w_i)} = \frac{dL_r(w_r)}{L_i(w_i)cos\theta _i dw_i}\]

转换下为:

\[dL_r(w_r) = f_r(w_i, w_r)L_i(w_i)cos\theta _idw_i\]

进行下积分:

\[L_r(w_r) = \int_\Omega f_r(w_i, w_r)L_i(w_i)cos\theta_idw_i\]

得到的\(L_r(w_r)\)是\(w_r\)方向的辐射出射度，方程（7）称为反射方程（ The Reflectance Equation）或者PBR的渲染方程（The Rendering Equation）。方程关于辐射的部分在文章的上半部分已经介绍了，现在来介绍下BRDF的\(f_r(w_i, w_r)\)是怎样计算的。首先我们需要微表面（microfacets）概念，因为PBR的反射方程是基于微表面得出的。

微观表面

BRDF认为表面是没有绝对平滑的，必然有一定程度上的粗糙度，从微观层面来讲这个表面是由一个一个的微平面构成的，这些微平面的法线各异，我们称这种平面叫做微观表面（microfacets）。由于表面存在粗糙度，微观平面做不到宏观表面那样入射光照完全和法线对称的角度发生反射，微观平面上反射出去的光比较杂乱无规则。如图[4]：

图[4] 左图是微观表面，右图是宏观表面（绝对光滑）

因为微观表面的凹凸不平，并不是所有反射出去的光能够进入视野，如下图[5]（暂不考虑二次反射）:

图[5]. 左图光照入射方向和视角方向比较接近，微表面的法线也是接近于视角方向的，结果是光照在微平面发射出来的光可以覆盖视角，所以从视角方向看到这部分表面是有光的。右图的情况正好相反导致从视角方向看不到表面的光照的。

BRDF对于微观表面的处理是在计算的时候加入一个粗糙度（roughness）的参数。表面的粗糙度越高，表示该表面凹凸不平的越严重，也就是微表面的法线越杂乱，那么表面反射出去的光照方向也就越不规则，实际表现出来就是整个表面看起来光照更加分散，而且光照的强度偏弱。表面的粗糙度越低，表示该表面越光滑，那么表面发射出去的关照方向更加接近一致。实际表现出来就是整个表面的光在正对着入射方向处的最明亮也比较集中，然后向四周慢慢扩散光的强度也随之慢慢降低。如下图[6]：

图[6]. 粗糙度由0.1到1.0的变化表现。

BRDF计算模型

BRDF将材质表面的光照反应分为两部分：

  • 漫反射（diffuse）：材质表面反射或者折射出去的比较杂乱的这部分光照。
  • 高光（specular）：材质表面以法线为中心的与入射光照对称角度反射出去的光照。

也就是说在BRDF的定义模型下，物体表面接受到光照之后会分两部分 可以用表达式表示为：

\[f_r(w_i, w_r) = f_{diffuse}(w_i, w_l) + f_{specular}(w_i, w_l)\]

如下图[7]所示:

图[7]. 入射光照在经过表面反射或者折射之后归为两种模型：漫反射（Diffuse）和高光（Specular）。

考虑到光传播的能量守恒，在光照射到材质表面的时候会由于材质的粗糙度的原因一定程度上会减弱反射出去的高光的强度，如图[8]：

图[8]. 入射光照如果只考虑一次反射的话，那么像左图的情况，光照就不会反射出任何光，相当于损失了。如果考虑二次反射的话是可以反射出去并且进入到视野的,如图右。

如果粗糙度比较严重的话，光照在材质表面需要经过很多次反射才能反射出去，甚至最终反射出去的光的出射角度并不能进入到视野中去。这部分光只能算作是光衰减的部分。基于此我们对计算BRDF的公式做出下面这样的改变：

\[f_r(w_i, w_r) = k_df_{diffuse}(w_i, w_r) + k_sf_{specular}(w_r, w_r)\]

其中\(k_d\)和\(k_s\)满足：

\[k_d + k_s \leq 1\]

介绍了BRDF的计算模型之后，接下来介绍下组成BRDF模型的漫反射和高光的具体计算方式。

BRDF的漫反射（Diffuse）

漫反射其实包括两部分，一部分是由于材质表面粗糙的原因光照经过多次反射最终反射出表面，但是出射的角度比较杂乱，如图[8]所描述的。另一部分则是材质的特殊性导致折射在材质的次表面（subsurface）的光线又折射出表面形成的关照。如图[9]：

图[9]. 部分折射的光照会最终折射出表面进入视野中。

但是不是所有的材质都会有这种现象，这个就是导体与电介质两种材质的区别了。纯金属材质（导体）没有在次表面发生散射的情况。这也是现实生活中导体材质的表面看起来光照更加强分布比较集中规则，而电介质材质的表面光照相对较弱的原因。

在游戏引擎中对漫反射光照的处理一般采用的是\(lambert\)计算模型。\(lambert\)模型的用如下公式表示：

\[f_{lambert} = \frac{\sigma}{\pi}\]

\(\sigma\)为漫反射率，除以\(\pi\)的得到半球的漫反射因子。代码中计算漫反射时把漫反射颜色乘以漫反射因子，代码如下：

1
2
3
4
5
6
float brdf_lambert()
{
    return _ReflectanceRatio / UNITY_PI;
}

float3 diffuse = diffuseColor * brdf_fd_lambert();

BRDF的高光（Specular）

BRDF的高光模型这里只介绍Cook-Torrance，这是目前实用比较广泛的模型。其他的还有Phong，Blinn-Phong等模型这里就不介绍了。先来看Cook-Torrance表达式：

\[f_{specular-cooktorrance} = \frac{D(h, \alpha) G(v, l, \alpha) F(v, h, f0)}{4(n \cdot v)(n \cdot l)}\]

整个公式由三部分内容组成：

  • D ：正态分布函数（Normal distribution function）
  • G：几何阴影函数（Geometric shadowing function）
  • F：菲涅尔（Fresnel）

正态分布函数

由于微表面存在粗糙度的原因，每个微表面的法线方向是没有规则比较杂乱的，正态分布计算的结果模拟的是各个微表面的法线与指定方向（视角方向和光照入射方向形成的中间向量）一致的分布情况。微表面的法线和指定方向越一致，那么这个微表面的光照越强，反之则越弱。先来看一个正态分布的一个样图：

图[10]. 正态分布样图

从图中可以看到深蓝色区域所占比率为全部数值的68%，它说明了什么呢？举个很浅显的例子，读书的时候每次班级的考试成绩的分布，成绩好的和成绩差的同学总是占少数，除此之外的同学的分数你会发现都比较集中，差距比较小。这部分分数集中的同学就是图[10]中的蓝色区域。这段小范围内集中了大部分的样本，具有这种分布规律的就是正态分布。那么为什么用正态分布函数来模拟计算微表面的粗糙度呢？很简单啊，因为经过实验表面微表面的法线分布情况正好接近于正态分布。

接着看正态分布的表达式（正态分布的表达式有很多，这里使用 Trowbridge-Reitz GGX）：

\[D_{GGX}(h, \alpha) = \frac{\alpha^2}{\pi ((n \cdot h)^2)(\alpha^2-1)+1)^2}\]

表达式中的各个变量的含义：

  • \(\alpha\)：粗糙度。
  • \(h\)：视角向量（或者光照的出射向量）和光照入射向量的中间向量（ \(half = normal + lightDir\)）。
  • \(n\)：法线向量。

转换成代码：

1
2
3
4
5
6
7
float brdf_specular_ndf_ggx(float NLhalf, float roughness)
{
    //这里的a并不是公式中的alpha，只是计算时的临时变量。
    float a = NLhalf * roughtness;
    float k = roughness / (1.0 - NLhalf * NLhalf + a * a);
    return k * k * (1.0 / PI);
}

代码里面计算的时候是把表达式展开来计算的，这样计算的好处在于减少了分母中不必要的相同的计算（k值的计算），计算更高效。

几何阴影函数

几何阴影函数计算的是光照在微平面被遮蔽形成的阴影的效果，如图[5]中右图，视角方向看过去的表面形成遮蔽，光照被微表面的凹凸起势正好挡住了，正好形成阴影。

几何阴影函数表达式：

\[G(v, l, \alpha) = \frac{2(n \cdot l)}{n \cdot l + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot l)^2}} \frac{2(n \cdot v)}{n \cdot v + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot v)^2}}\]

表达式中的各个变量的含义：

  • \(v\)：视角向量。
  • \(l\)：光照向量。
  • \(n\)：法线向量。
  • \(\alpha\)：粗糙度。

之前看Unity的BRDF渲染的着色器的代码的时候一直不明白它的计算代码，它的计算代码是这样的（省略了很多细节代码）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// Main Physically Based BRDF
// Derived from Disney work and based on Torrance-Sparrow micro-facet model
//
//   BRDF = kD / pi + kS * (D * V * F) / 4
//   I = BRDF * NdotL
//
half4 BRDF1_Unity_PBS (half3 diffColor, half3 specColor, half oneMinusReflectivity, half smoothness,
	half3 normal, half3 viewDir,
	UnityLight light, UnityIndirect gi)
{
    ...
#if UNITY_BRDF_GGX
	half V = SmithJointGGXVisibilityTerm (nl, nv, roughness);
	half D = GGXTerm (nh, roughness);
#endif
    half specularTerm = V*D * UNITY_PI; // Torrance-Sparrow model, Fresnel is applied later
    ...
    half3 color =   diffColor * (gi.diffuse + light.color * diffuseTerm)
                    + specularTerm * light.color * FresnelTerm (specColor, lh)
					+ surfaceReduction * gi.specular * FresnelLerp (specColor, grazingTerm, nv);

	return half4(color, 1);
}

通过函数说明可以看到Unity计算BRDF的公式

\[BRDF = \frac{ \frac{kD} {\pi} + kS (D V F) }4\]

不明白为啥高光部分计算\(D V F\)，\(V\)和\(G\)究竟是什么关系？特地查找了资料发现有人也在问这个问题where-come-from-about-unity-brdf-function，可惜回答里没有给出真正的具体的答案来解释清楚这个问题。其实很简单，上面给出了几何阴影函数之后我们可以带入到高光计算函数（现在还没介绍\(Fresnel\)，没有任何关系，而且\(Fresnel\)很好理解）。带入到高光计算函数中你会发现，高光计算函数的分母和几何阴影函数的分子\(4(n\cdot l)(n \cdot v)\)正好可以抵消掉，抵消掉之后我们用一个全新的符号来代替几何阴影函数，那就用\(V\)吧。全新的高光计算函数：

\[f_{specular-cooktorrance} = D(h, \alpha) V(v, l, \alpha) F(v, h, f0)\]

Unity的BRDF的公式就是这样得来的，得到的新的几何阴影函数如下：

\[V(v, l, \alpha) =  \frac{1}{n \cdot l + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot l)^2}}  \frac{1}{n \cdot v + \sqrt{\alpha^2 + (1-\alpha^2)(n\cdot v)^2}}\]

用代码表示如下：

1
2
3
4
5
6
7
8
9
10
11
12
float brdf_specular_gsf_smith(float dotV, float roughness2)
{
    return = 1 /(dotValue + sqrt(dotV * dotV * (1 - roughness2) + roughness2));
}

float brdf_specular_gsf_ggx(float NdotL, float NdotV, float roughness)
{
    float a2 = roughness * roughness;
	float ggx_l = brdf_specular_gsf_smith(NdotL, a2);
    float ggx_v = brdf_specular_gsf_smith(NdotV, a2);
    return ggx_l * ggx_v;
}

菲涅尔

先来看一张湖面景色图片：

图[11]

图[11]

从上面的湖面景色图片中我们可以发现，距离山越近的地方水面倒影的颜色越深，距离视角位置越近倒影的颜色越浅，水下的石头也更清晰些。这种现象其实就是菲涅尔现象或者叫菲涅尔反射。菲涅尔反射描述光在两种不同折射率的介质中传播时的反射的值，通过这个值我们可以计算当光照照射到表面时，表面所反射的光的量。可以先了解下方程，这里使用 Schlick近似菲涅尔方程（一般光照计算都采用这个近似方程）： \(R(\theta) = R_0 + (R_{90} - R_0)(1-cos\theta)^5\)

  • \(R_0\)：光照垂直入射到材质表面时的反射比，这个值是个常数。
  • \(cos\theta\)：材质表面的法线向量和视角向量的余弦值。

根据公式我们可以得出反射比 \(R{\theta}\) 和视角方向有很大的关系，再来解释下图[11]中的现象。距离视角位置越远的水面位置，视角和该点位置的夹角越小，那么余弦值就越小，得出的反射比就越小。所以你看到的水面倒影越清晰，看不清水下的石头。用一张说明图来描述下，如图[12]：

图[12]

可以从近视点位置的A点和远视点位置的B来对比下反射比可以明白图[11]中的现象了。

对于菲涅尔方程中的\(R_0\)值，这个值是根据材质来定的。显示世界中一些比较常见材质的\(R_0\)值和\(cos\theta\)的菲涅尔反射比关系图如下：

图[13]

在视角向量和材质表面法线向量角度趋于\(90^\circ\)度时任何材质的反射比都趋近于1，这样在菲涅尔方程中的\(R_{90}\)我们直接可以用常数1替换。

菲涅尔反射就介绍这些，下面我们把菲涅尔反射方程转换为程序代码：

1
2
3
4
5
float3 brdf_fresnel_schlick(float NdotL, float3 R0)
{
    //1.0是90度时候的反射比
    return R0 + (float3(1.0, 1.0, 1.0) - R0) * pow(1 - NdotL, 5.0);
}

BRDF的内容都介绍完成了。PBR方程中现在只剩下一个内容没有提到，\(L_e(p, w)\)。放到Unity中，我们可以看看Unity的采用PBR渲染方式的Standard Shader ：

Unity里面把它当作一个材质本身一个发射的颜色，这个颜色包括自定义一个预置颜色和全局环境光照的颜色。这是一个可选项，一般简单处理的话这个值不需要也可以。

总结

到这里整个PBR的内容都介绍完成了，其实内容并不多，花费一些时间肯定能完全理解。后续我再整理出一个基于Unity实现的PBR功能的demo。

参考：

  1. Wiki Physically based rendering
  2. 3dcoat pbr
  3. Google filament
  4. scratchapixle mathematics of shading
  5. article_physically_based_rendering_cook_torrance
  6. article_physically_based_rendering
  7. learnopengl
  8. Bidirectional_reflectance_distribution_function
  9. 正态分布
  10. 菲涅耳方程 milo
  11. 菲涅尔方程 wiki
  12. Schlick’s approximation
阅读全文 »